
98
C A P I T O L O 4
Conduttori. Dielettrici. Energia elettrostatica
in buon accordo con i valori sperimentali per quelle sostanze come l’argon
κ
= 1.000545,
l’azoto
κ
= 1.000580, l’elio
κ
= 1.000068, l’idrogeno
κ
= 1.000264, in cui il meccanismo di
polarizzazione elettronica è l’unico presente.
Polarizzazione per orientamento
Alcune molecole poliatomiche, come acqua, H
2
O, figura 4.49, e acido cloridrico,
HCl, possiedono un momento di dipolo intrinseco
p
0
, per cui sono dette
polari
. Tali
molecole sono formate da due o più atomi, di specie diversa, disposti secondo confi-
gurazioni in cui il centro della carica negativa non coincide con quello della carica
positiva. Nella molecola d’acqua il centro della carica positiva sta praticamente nel
punto di mezzo della congiungente i due atomi di idrogeno, mentre quello della ca-
rica negativa coincide quasi con il nucleo di ossigeno; ne deriva un momento di di-
polo elettrico
p
0
che vale circa 6 · 10
–30
cm.
In assenza di campo elettrico i singoli dipoli sono diretti casualmente in tutte le di-
rezioni così che in ogni elemento di volume
d
τ
il momento di dipolo elettrico risultante
è eguale a zero e quindi la polarizzazione è nulla. Quando si applica un campo elettrico
E
dall’esterno ha luogo la polarizzazione elettronica, ma succede anche che su ogni di-
polo permanente
p
0
agisce il momento meccanico (2.49)
M
=
p
0
×
E
che tende a orientare
p
0
concordemente a
E
. Se tutte le molecole si allineassero risulte-
rebbe una polarizzazione intensa; però a temperature
T
ordinarie e con campi elettrici
non particolarmente intensi gli urti tra le molecole dovuti all’agitazione termica per-
mettono un allineamento soltanto parziale che si rappresenta con un
momento di dipolo
medio
<
p
>, parallelo ad
E
e ad esso proporzionale.
Lo studio del comportamento statistico di un insieme di dipoli alla temperatura
T
e
sottoposti all’azione di un campo elettrico
E
ha permesso a P. Debye di calcolare <
p
>.
Per campi elettrici normali e temperature
T
non troppo basse risulta
p
2
0
<
p
> = –––––
E
,
(4.48)
3
k
B
T
con
k
B
= 1.38 · 10
–23
J/K costante di Boltzmann. Pertanto la polarizzazione (4.35) vale
np
2
0
P
=
n
<
p
> =
ε
0
––––––
E
;
(4.49)
3
ε
0
k
B
T
anche in questo caso la (4.37) è verificata. Come era da attendersi la polarizzazione è in-
versamente proporzionale alla temperatura
T
: al crescere della temperatura gli urti tra
le molecole accentuano il disallineamento rispetto al campo elettrico
E
. Dal confronto
con (4.37) si trova per la suscettività elettrica l’espressione
np
2
0
χ
p
= –––––– .
(4.50)
3
ε
0
k
B
T
La dipendenza di
χ
p
da 1/
T
prende il nome di
legge di Curie
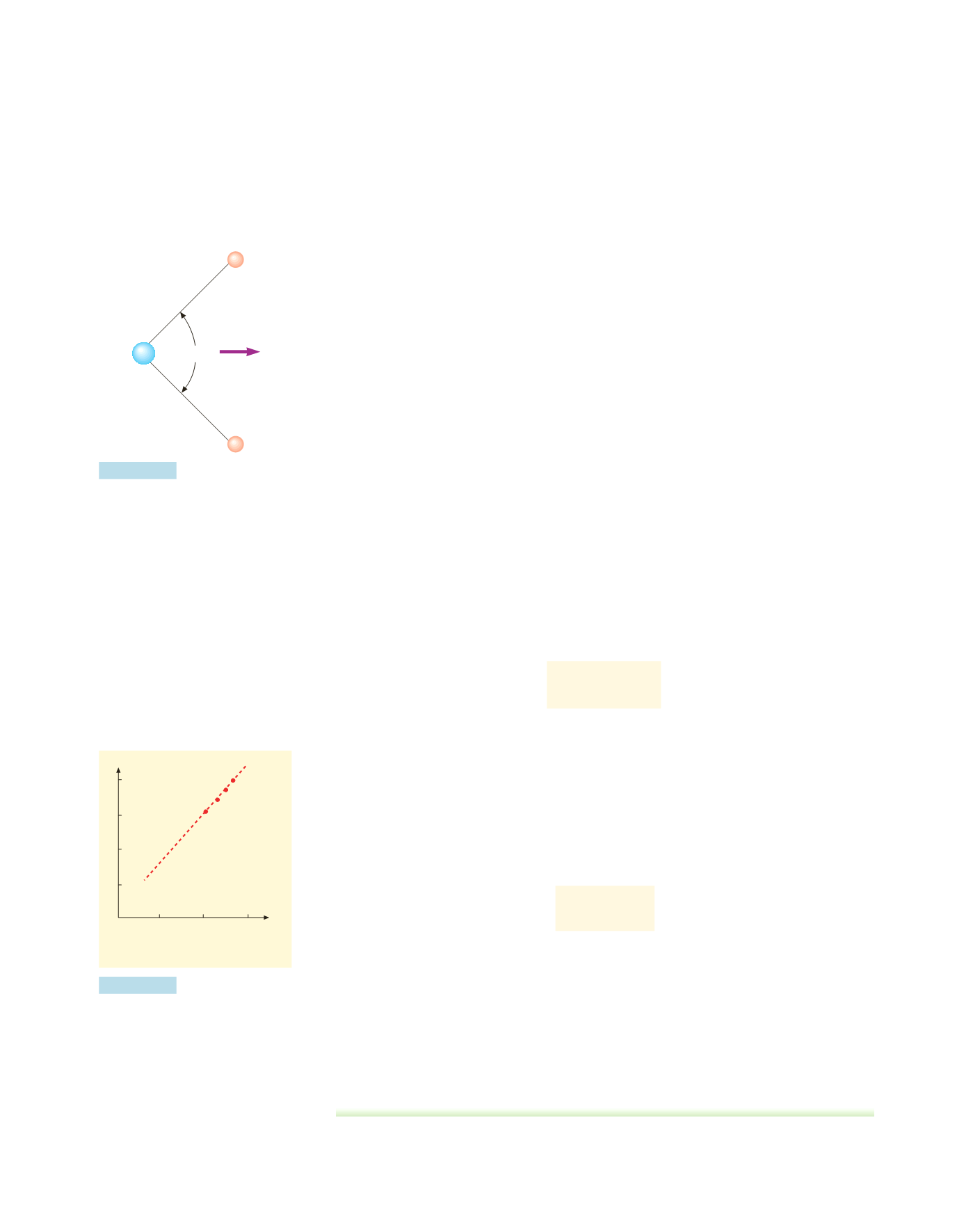
. La suscettività elettrica
del vapor d’acqua è stata misurata in funzione della temperatura: i dati sperimentali
sono riportati in figura 4.50 e si vede che la dipendenza da 1/
T
è ben verificata. Dalla
pendenza della curva si ricava
np
2
0
/3
ε
0
k
B
= 1.46 K; noto il numero di molecole per unità
di volume
n
= 1.38 · 10
25
m
–3
, è possibile calcolare il momento di dipolo elettrico della
molecola d’acqua, che risulta
p
0
= 6.25 · 10
–30
Cm. La suscettività elettrica alla tempera-
tura
T
= 393 K = 120°C vale
χ
p
= 1.46/393 3.7 · 10
–3
→
κ
= 1 +
χ
= 1.0037 .
_
_
+
+
H
O
H
p
0
105°
4
3
2
1
0
10
–3
2 · 10
–3
3 · 10
–3
1/
T
(K
–1
)
χ
· 10
3
Molecola d’acqua.
Figura 4.49
Suscettività elettrica del vapore
d’acqua.
Figura 4.50
















