
4.7 Polarizzazione dei dielettrici
93
Senza approfondire oltre la dinamica dei meccanismi di polarizzazione, riassu-
miamo l’effetto dell’applicazione di un campo elettrostatico ad un dielettrico di-
cendo che ciascun atomo o molecola acquista un momento di dipolo elettrico me-
dio <
p
>, parallelo e concorde a
E
.
Considerato un volumetto
τ
nell’intorno di un punto
O
in cui sono contenuti
N
atomi (o molecole), il momento di dipolo risultante
p
è dato da
p
=
N
<
p
> e il
momento di dipolo per unità di volume nell’intorno del punto
O
si scrive
p
N
P
= –– = –– <
p
> =
n
<
p
> ,
(4.35)
τ
τ
dove
n
è il
numero di atomi
(
o molecole
)
per unità di volume
. Dato che ciascun mo-
mento di dipolo <
p
> è parallelo al campo
E
, anche
P
, detto
vettore polarizzazione
,
è parallelo a
E
.
Riprendiamo in considerazione il condensatore piano carico con all’interno
una lastra di dielettrico, che supponiamo
polarizzato uniformemente
: il
vettore polariz-
zazione
P
è cioè costante in tutti i punti della lastra.
Suddividiamo la lastra in prismi infinitesimi di base
d
Σ
0
, altezza
dh
e volume
d
τ
=
d
Σ
0
dh
, figura 4.43a: ciascuno di questi ha, secondo (4.35), il momento di dipolo
E
E
= 0 , <
p
> = 0
p
0
(a)
(b)
<
p
> | |
E
+
+
+
+
_
_
_
_
+
+
+
+
_
_
_
_
+ + + +
_ _ _ _
d
Σ
0
dh
–
dq
p
+
dq
p
(a)
(c)
(b)
P
P
+
dq
p
–
dq
p
dq
p
= 0
–
σ
p
= –
P
+
σ
p
=
P
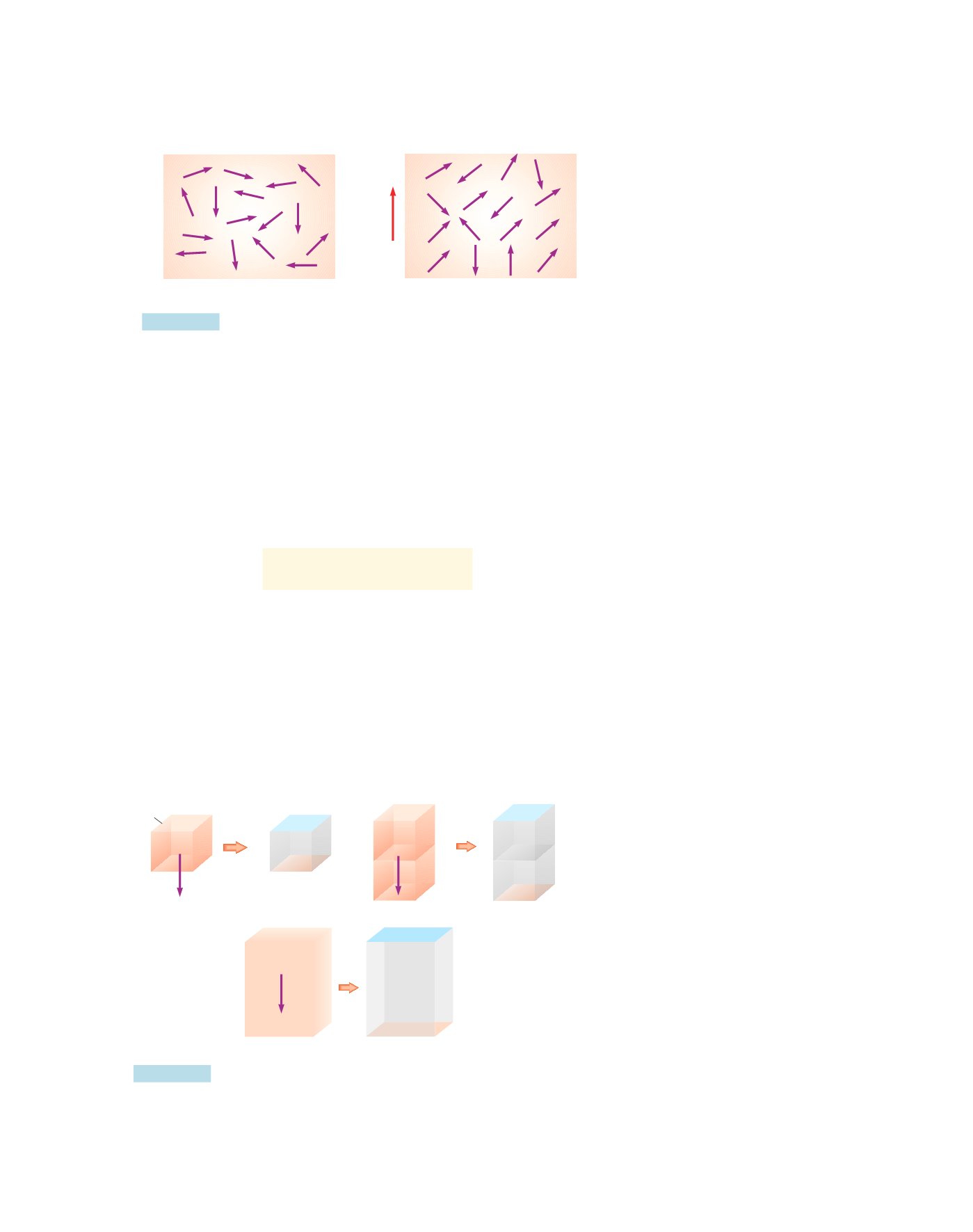
Azione del campo elettrostatico sulle molecole di una sostanza dotate di
momento di dipolo elettrico intrinseco.
Rappresentazione schematica della formazione della carica di polarizzazione
sulle superficie di una lastra piana di materiale dielettrico.
Figura 4.42
Figura 4.43
p
0
p
0
P
Vettore polarizzazione
















