
90
C A P I T O L O 4
Conduttori. Dielettrici. Energia elettrostatica
Un condensatore piano, con armature di area
Σ
distanti
h
,
è caricato con una carica
q
0
e quindi isolato. Una lastra di die-
lettrico, di costante dielettrica relativa
κ
, area
Σ
e spessore
s
, è
posta all’interno, come mostrato in figura 4.35. Calcolare la
differenza di potenziale tra le armature e la capacità equiva-
lente del sistema.
Soluzione
Il campo elettrostatico all’interno del dielettrico è
dovuto sia alle cariche libere, distribuite sulle armature con
densità
σ
0
, che a quelle che compaiono sulle facce della lastra
ed ha l’espressione (4.24):
E
κ
=
σ
0
/
ε
0
κ
. Il campo nei punti in
cui non c’è la lastra è determinato solamente dalla densità di
carica libera, poiché, in base ai risultati degli esempi 1.8 e 2.8,
le due distinzioni di carica +
σ
p
e –
σ
p
danno risultato nullo
all’esterno:
E
0
=
σ
/
ε
0
. La differenza di potenziale è
V
κ
=
∫
h
0
E
·
d
h
=
E
0
(
h
–
s
) +
E
κ
s
,
qualunque sia la posizione della lastra rispetto alle armature.
Introduciamo il valore dei campi elettrostatici:
σ
0
σ
0
σ
0
h
κ
– 1
s
V
κ
= –– (
h
–
s
) + –––
s
= –––– 1 – –––––– –– =
ε
0
κ ε
0
ε
0
κ
h
κ
– 1
s
V
κ
=
V
0
1 – –––––– ––
κ
h
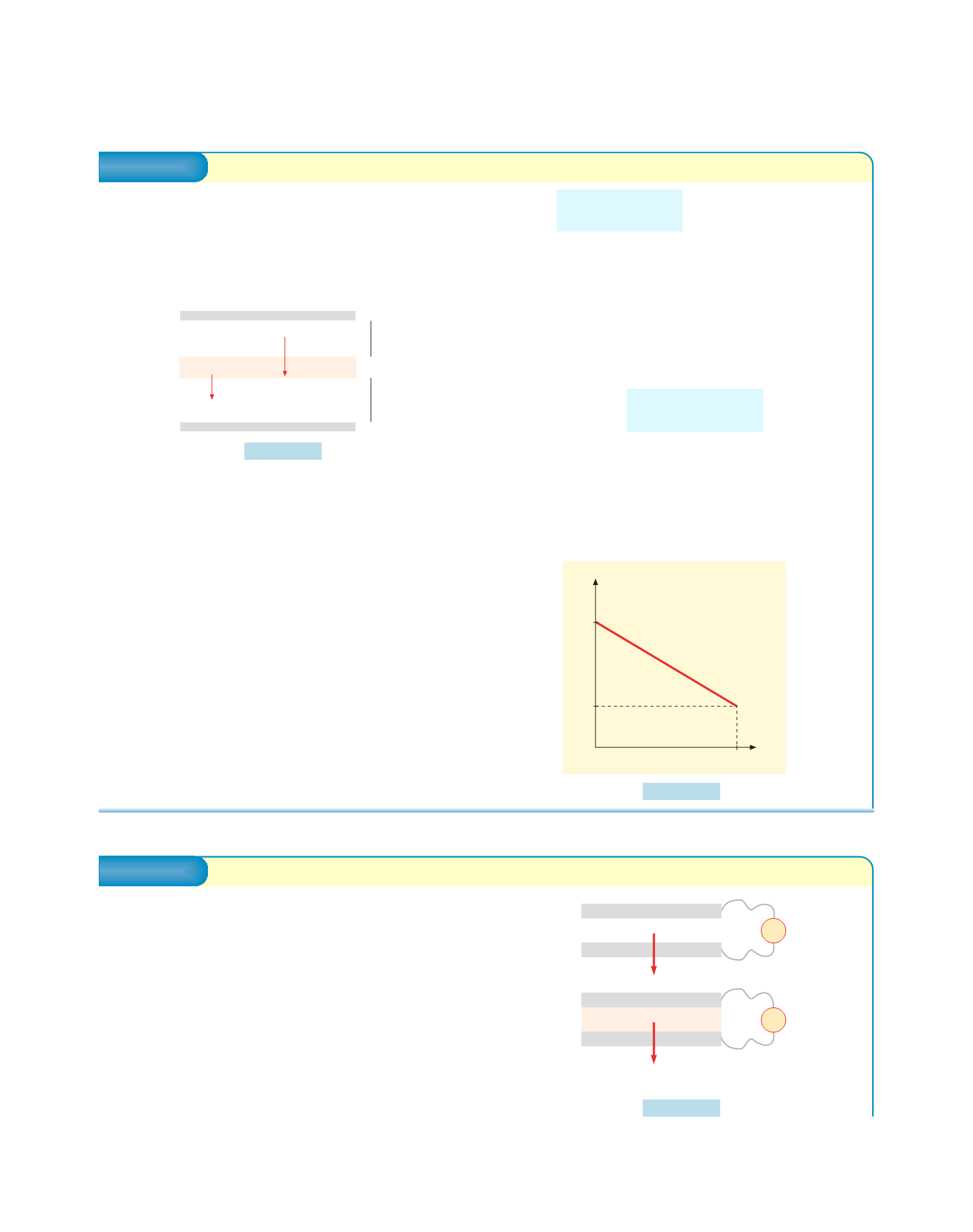
con variazione lineare tra
V
0
(
s
= 0) e
V
κ
=
V
0
/
κ
(
s
=
h
), figura
4.36.
La d.d.p. si può riscrivere
σ
0
Σ
κ
– 1
V
κ
= ––––
h
– ––––––
s
,
ε
0
Σ
κ
in cui
σ
0
Σ
è la carica libera
q
presente sulle armature. Pertanto
V
κ
1
h
–
s
s
–– = –– = ––––– + –––––– ,
q C
ε
0
Σ
ε
0
κ Σ
dove
C
è la
capacità equivalente
del condensatore parzialmente
riempito di dielettrico. Si vede dalla formula che la capacità
equivalente non dipende dalla posizione della lastra e che il si-
stema si può interpretare come due condensatori in serie, uno
vuoto con capacità
ε
0
Σ
/(
h
–
s
), l’altro con dielettrico, di capa-
cità
ε
0
κ Σ
/
s
.
E
SEMPIO
4.11
Lastra di dielettrico all’interno di un condensatore piano
_
_
_
_
_
+ + + + +
+ + + + +
_
_
_
_
_
s
E
κ
κ
h
E
0
Un condensatore piano, con armature di area
Σ
distanti
h
,
viene collegato ad un generatore che mantiene una differenza
di potenziale
V
0
tra le armature. Una lastra di dielettrico di co-
stante dielettrica relativa
κ
viene inserita tra le armature, riem-
piendo completamente il volume, figura 4.37. Descrivere le
proprietà elettrostatiche del sistema prima e dopo l’inseri-
mento della lastra, ammettendo che anche in questo caso la
capacità aumenti di un fattore
κ
.
Soluzione
Nella condizione senza dielettrico:
ε
0
Σ
V
0
σ
0
C
0
= –––– ,
q
0
=
C
0
V
0
,
E
0
= –– = –– ,
h
h
ε
0
E
SEMPIO
4.12
Lastra di dielettrico tra armature di un condensatore piano collegato ad un generatore
Figura 4.35
Figura 4.36
V
V
0
1
V
0
–––
κ
s
––
h
V
0
V
0
E
0
E
0
Figura 4.37
















