
1
1
U
e
= ––
C
0
V
2
0
,
u
e
= ––
ε
0
E
2
0
.
2
2
Nella condizione con dielettrico, dato che
C
=
κ
C
0
, si ha:
V
0
q
=
CV
0
=
κ
q
0
,
σ
=
κ σ
0
,
E
=
E
0
= –– ,
h
κ
– 1
q
p
= ––––––
q
= (
κ
– 1)
q
0
=
q
–
q
0
,
σ
p
= (
κ
– 1)
σ
0
,
κ
1
1
U
e
= ––
CV
2
0
=
κ
U
e
,
u
e
= ––
ε
E
2
0
=
κ
u
e
.
2
2
In un condensatore piano, le cui armature quadrate sono
di lato
l
e distano
h
, è parzialmente inserita per un tratto
x
una
lastra di dielettrico, di costante dielettrica
κ
e spessore
h
. Un
generatore mantiene la differenza di potenziale
V
costante tra
le armature. Calcolare la forza
F
con cui la lastra è risucchiata
all’interno del condensatore, il lavoro
W
complessivo fatto
dalla forza
F
e l’energia
U
gen
erogata dal generatore durante il
processo. Eseguire i calcoli per
l
= 20 cm,
h
= 1 cm,
κ
= 4,
V
= 500 V.
Soluzione
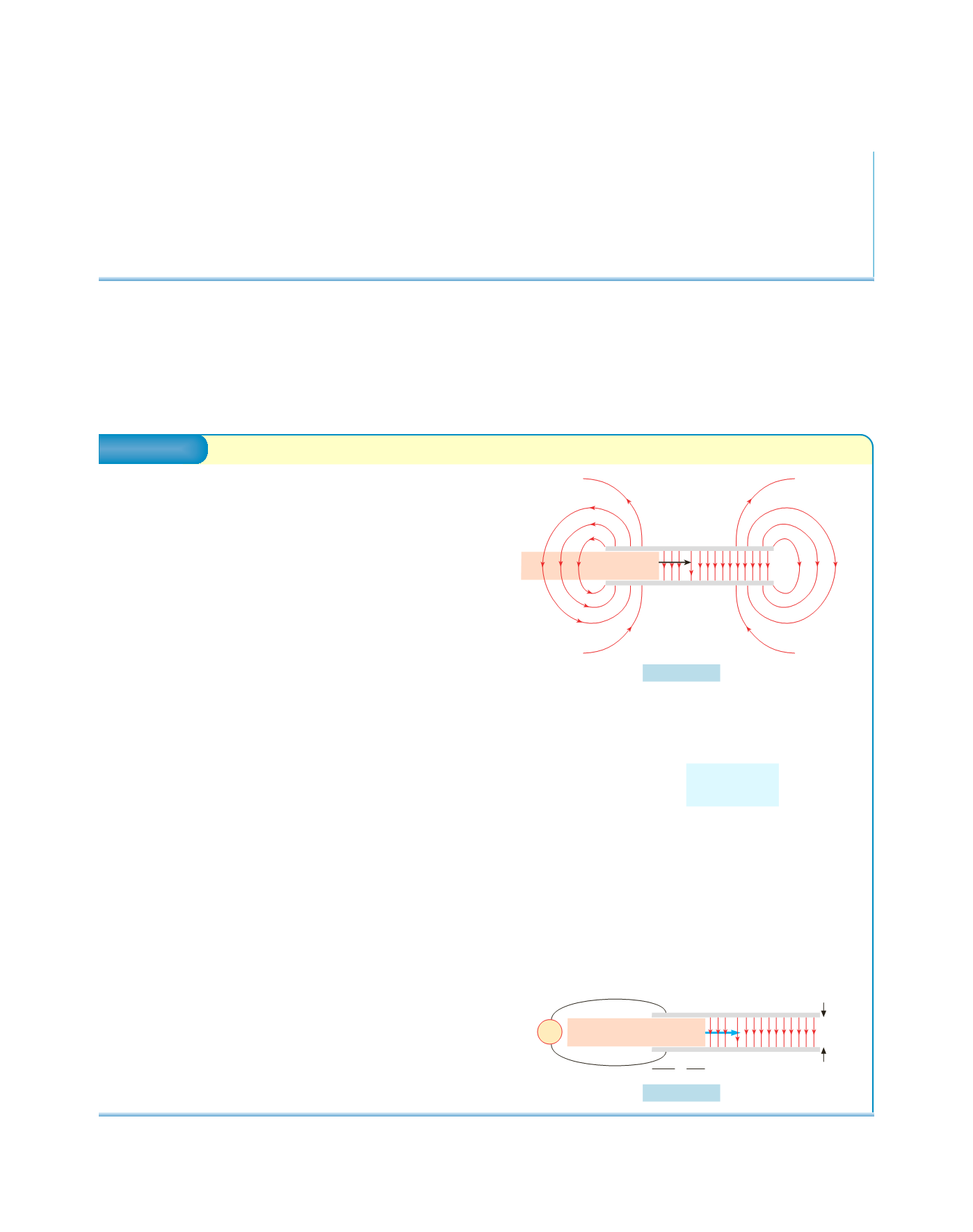
Con riferimento alla figura 4.38 puntualizziamo
che è il campo elettrostatico non uniforme in prossimità dei
bordi del condensatore che produce la forza
F
di risucchio.
Tale campo agisce sulle cariche superficiali indotte sul dielet-
trico, che non sono distribuite uniformemente. Il processo è
schematizzato come in figura 4.39; si calcola innanzitutto la ca-
pacità equivalente del sistema, pensato come due condensa-
tori in parallelo, uno con dielettrico e uno senza dielettrico:
ε
0
κ
ε
0
l
(
l
–
x
)
C
(
x
) = ––––
lx
+ ––––––––– .
h
h
Per un avanzamento
dx
della lastra dielettrica la capacità
aumenta di
dC
ε
0
(
κ
– 1)
l
dC
= –––
dx
= ––––––––––
dx
,
dx
h
a cui corrisponde una variazione di carica
dq
=
V dC
operata dal
generatore, che la sposta da un’armatura all’altra con spesa di
lavoro
dW
gen
=
V dq
=
V
2
dC
. D’altra parte l’energia elettrosta-
1
1
tica aumenta di
dU
e
= ––
dC V
2
= ––
dW
gen
. Il lavoro fornito dal
2
2
generatore va dunque per metà in aumento di energia elettro-
statica e per metà in lavoro della
forza di risucchio
:
1
dW
=
F dx
=
dW
gen
–
dU
e
=
dU
e
= ––
V
2
dC
;
2
da qui si ricava:
dU
e
ε
0
(
κ
– 1)
l V
2
F
= –––
V
= cost
= ––––––––––––– :
dx
2
h
la forza non dipende dalla posizione
x
della lastra. Numerica-
mente
F
= 6.64 · 10
–5
N. Il lavoro complessivo della forza è
W
=
Fl
= 1.33 · 10
–5
J, l’aumento di energia elettrostatica è
eguale, il generatore fornisce il lavoro
U
gen
= 2
W
= 2.66 · 10
–5
J,
a spese della propria energia interna che diminuisce di una
eguale quantità.
E
SEMPIO
4.13
Forza di risucchio di una lastra di dielettrico
V
x
h
F
κ
4.6 Dielettrici. La costante dielettrica
91
Figura 4.39
Figura 4.38
+
q
F
κ
–
q
















