
densità di carica
σ
= 8.86 · 10
–6
C/m
2
. La densità di carica
di polarizzazione
σ
P
sulla superficie dell’isolante di raggio
R
è
σ
P
= 0.75
σ
. Calcolare: a) la costante dielettrica relativa
κ
dell’isolante, b) il campo elettrostatico
E
1
in un punto
all’interno del dielettrico a distanza
r
1
= 2 cm dal centro e
c) a quale distanza
r
2
, al di fuori dell’isolante,
E
2
=
E
1
.
4.39
Due condensatori, di capacità
C
1
= 200 pF e
C
2
= 10
3
pF,
collegati in parallelo, vengono caricati ad una differenza
di potenziale
V
= 400 V e quindi isolati. Successivamente
lo spazio tra le armature di
C
1
viene completamente riem-
pito di acqua distillata, contenuta in un sottile conteni-
tore (
κ
= 80). Calcolare: a) la variazione
D
V
della diffe-
renza di potenziale tra
A
e
B
e b) la variazione della carica
D
q
1
sulle armature di
C
1
.
4.40
A due condensatori piani di capacità
C
1
= 500 pF e
C
2
=
1000 pF, collegati in serie, è collegato un generatore che
mantiene una differenza di potenziale costante
V
= 400 V.
Una lastra di dielettrico, con costante dielettrica relativa
κ
= 4, viene inserita tra le armature di
C
1
, così da riem-
pirlo completamente. Calcolare: a) la variazione di carica
D
q
erogata dal generatore, b) la variazione
D
V
1
della dif-
ferenza di potenziale ai capi di
C
1
e c) l’energia
W
gen
for-
nita dal generatore nel processo.
4.41
Tre sottili gusci conduttori di forma sferica, concentrici e
di raggi rispettivamente
R
1
= 10 cm,
R
2
= 20 cme
R
3
= 40 cm,
sono stati caricati rispettivamente con carica
q
1
= 10
–8
C,
q
2
= 3
q
1
e
q
3
= 5
q
1
. Lo spazio tra
R
1
e
R
2
viene completamente
riempito di dielettrico di costante dielettrica relativa
κ
= 4.
Calcolare: a) il campo elettrico
E
(
r
) alla distanza
r
= 50 cm
dal centro
O
comune e b) la differenza di potenziale
D
V
tra il conduttore interno e quello esterno.
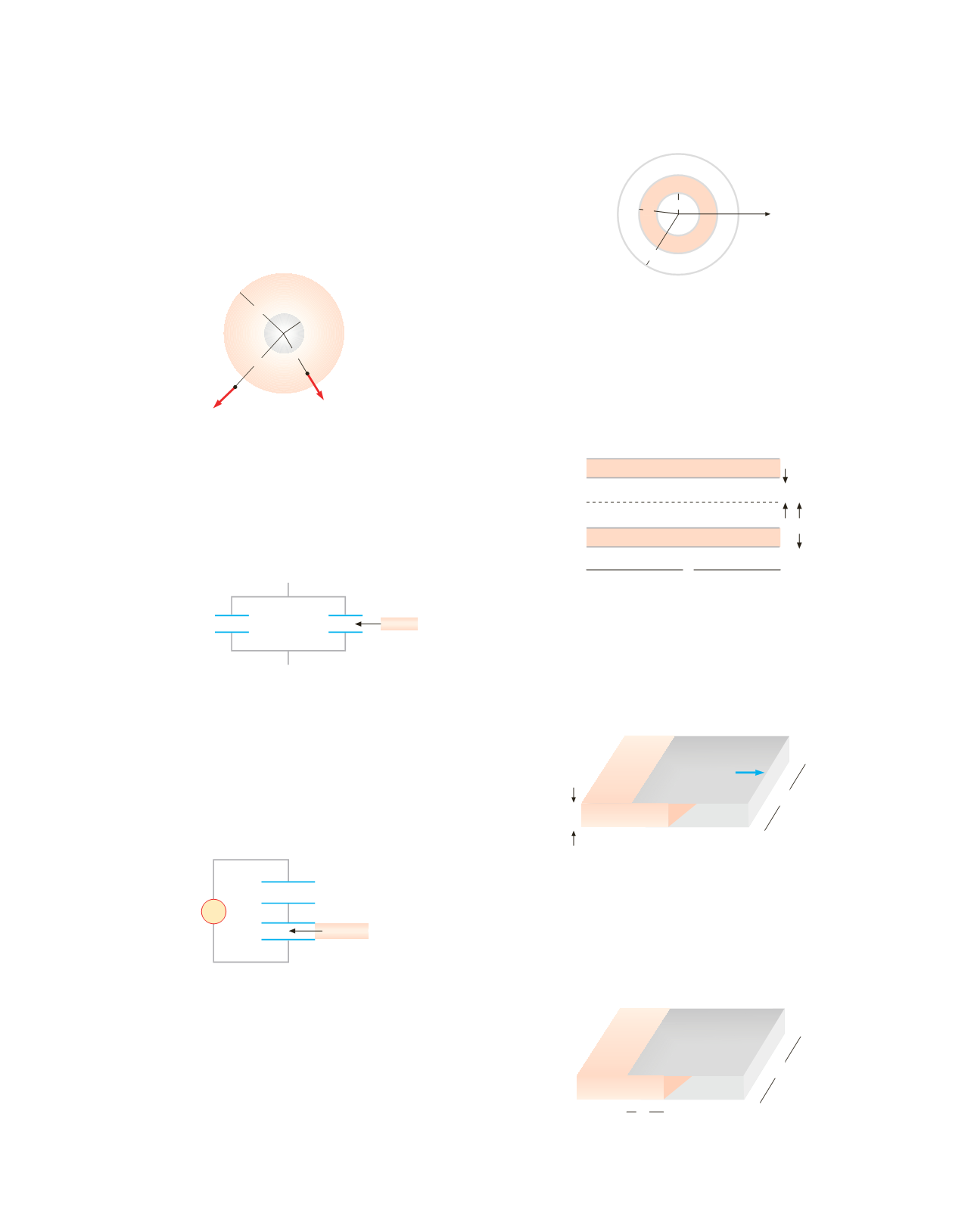
4.42
Un condensatore cilindrico, con armature di raggio
R
1
=
5 mm e
R
2
= 10 mm, lunghe
l
= 15 cm, è completamente
riempito di un materiale isolante avente costante dielet-
trica relativa
κ
= 2.8. Esso è stato caricato con una carica
q
= 2 nC. Calcolare: a) la densità di carica
σ
i
e il campo
elettrostatico
E
i
su ciascuna armatura, b) la differenza di
potenziale
D
V
tra le armature e c) la carica di polarizza-
zione
q
P
che si forma sulle superficie del dielettrico.
4.43
Un condensatore piano ha armature quadrate di lato
l
=
20 cm, distanti
d
= 5 mm ed è caricato con una carica
q
=
2 · 10
–8
C. Una lastra di materiale isolante delle stesse di-
mensioni dello spazio interno del condensatore e
κ
= 2.6,
viene avvicinata al condensatore. Calcolare la forza media
F
m
con cui la lastra viene risucchiata completamente al-
l’interno del condensatore.
R
2
R
1
l
l
V
d
E
1
E
2
r
1
r
2
R
κ
A
B
C
1
C
2
κ
C
2
C
1
κ
r
R
1
R
2
R
3
κ
κ
d
F
m
κ
Problemi
105
4.44
Un condensatore piano con armature quadrate di lato
l
distanti
d
, è riempito per un tratto
x
da una lastra iso-
lante, di costante dielettrica relativa
κ
ed è carico con una
carica
q
. Calcolare: a) la capacità
C
(
x
) del condensatore,
b) l’energia elettrostatica
U
e
(
x
) e la forza
F
(
x
) che agisce
sulla lastra e in particolare quando è a metà, per
l
= 10
cm,
d
= 0.5 cm,
κ
e
= 2 e
q
= 10
–8
C.
l
x














