
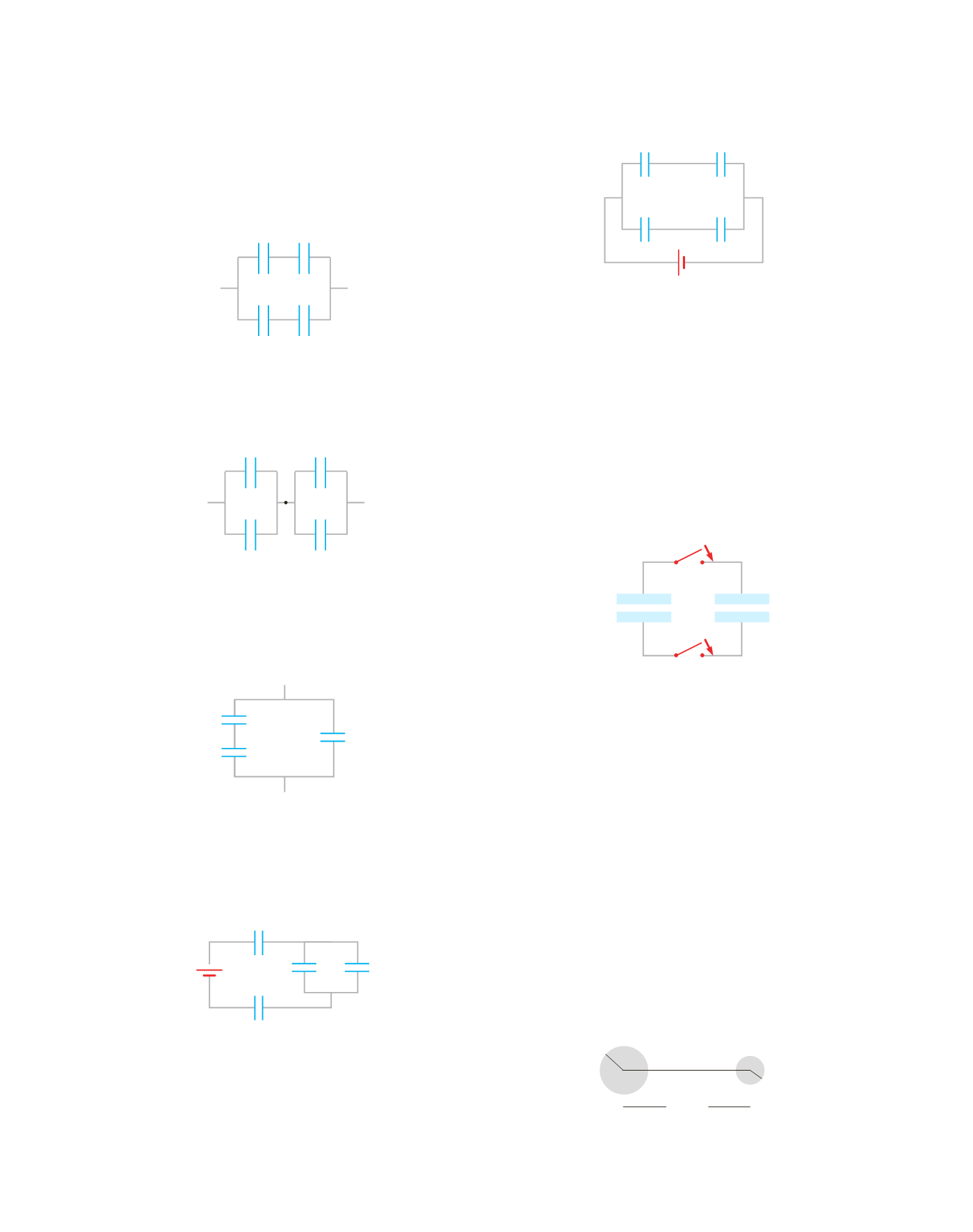
4.17
In figura
C
1
= 20 pF,
C
2
= 40 pF,
C
3
= 30 pF,
C
4
= 60 pF e la
carica sul condensatore
C
1
vale
q
1
= 200 pC. Calcolare: a)
la differenza di potenziale
D
V
tra i punti
A
e
B
e b) la ca-
rica
q
i
sui rispettivi condensatori
C
i
.
4.18
In figura
C
1
= 20 pF,
C
2
= 40 pF,
C
3
= 30 pF,
C
4
= 60 pF e la
carica sul condensatore
C
1
vale
q
1
= 200 pC. Calcolare: a)
la differenza di potenziale
D
V
tra i punti
A
e
B
e b) la ca-
rica
q
i
sui rispettivi condensatori
C
i
.
4.22
Dopo aver caricato due condensatori di capacità
C
1
= 5
μ
F
e
C
2
= 4
μ
F rispettivamente alla differenza di potenziale
V
1
= 300 V e
V
2
= 250 V, si collegano tra loro le armature po-
sitive e le armature negative e viene posto in parallelo ai
primi un condensatore
C
= 1
μ
F. Calcolare: a) la carica
q
i
presente alla fine su ciascun condensatore e b) la varia-
zione
D
U
e
di energia elettrostatica nel processo.
4.23
Due condensatori
C
1
= 120 pF e
C
2
= 240 pF sono caricati
tramite una batteria ciascuno ad una differenza di poten-
ziale
V
= 200 V. I due condensatori vengono collegati tra
loro, l’armatura positiva dell’uno con la negativa dell’al-
tro. Calcolare: a) la differenza di potenziale
V
ai capi del
sistema e b) la variazione di energia elettrostatica
D
U
e
.
4.24
Due sfere conduttrici
C
1
e
C
2
, rispettivamente di raggi
R
1
= 6 cm e
R
2
= 12 cm, hanno la stessa carica
q
= 6 · 10
–8
C e
sono molto distanti. Le due sfere vengono collegate tra
loro con un filo sottile. Calcolare; a) le cariche
q
1
e
q
2
sui
conduttori e b) il numero di elettroni
N
e
trasferiti da un
conduttore all’altro.
4.25
Due piccole sfere conduttrici identiche cariche
q
1
e
q
2
si at-
traggono con la forza
F
1
= 0.108 N, quando sono a distanza
r
= 50 cm. Le due sfere vengono collegate con un filo sotti-
lissimo conduttore, che viene quindi rimosso. Le sfere ora
si respingono con una forza
F
2
= 0.036 N. Calcolare
q
1
e
q
2
.
4.26
Due sfere conduttrici di raggi rispettivamente
R
1
= 6 mm
e
R
2
= 4 mm, sono poste a distanza
d
>>
R
1
. Una carica
q
=
10
–10
C viene comunicata alla prima sfera; successiva-
mente le due sfere vengono collegate con un filo sottilis-
simo conduttore. Calcolare: a) la carica
q
1
e
q
2
sulle due
sfere, b) il potenziale
V
delle due sfere, c) il campo elet-
trostatico
E
1
e
E
2
sulla superficie delle due sfere e d)
l’energia elettrostatica
D
U
e
persa nel collegamento.
4.19
Nella figura
C
1
= 2
μ
F,
C
2
= 6
μ
F,
C
3
= 3.5
μ
F e la tensione
minima alla quale si innesca la scarica in ciascun conden-
satore è rispettivamente
V
1
= 100 V,
V
2
= 50 V e
V
3
= 400 V.
Calcolare la massima differenza di potenziale
V
max
possi-
bile tra i punti
A
e
B
.
4.20
Si consideri il sistema di condensatori di figura,
C
1
= 2 nF,
C
2
= 3 nF,
C
3
= 5 nF e
C
4
= 4 nF, collegati ad un generatore
con
V
0
= 15 V. Calcolare: a) la capacità equivalente
C
eq
tra
i punti
A
e
B
, b) la carica
q
i
su ciascun condensatore e c)
l’energia elettrostatica
U
e
del sistema.
4.21
Nel sistema di condensatori di figura,
C
1
= 20 nF,
C
2
= 40
nF,
C
3
= 50 nF,
C
4
= 30 nF e
V
0
= 90 V.Calcolare: a) la capa-
cità equivalente
C
eq
del sistema tra i punti
P
e
Q
, e b) la dif-
ferenza di potenziale
V
i
ai capi di ciascun condensatore.
+ + + + +
_ _ _ _ _
+ + + + +
_ _ _ _ _
C
1
C
2
C
3
C
4
B
A
C
1
C
2
C
3
C
4
A
B
C
C
1
C
2
C
3
A
B
V
0
C
1
C
2
C
4
C
3
A
B
C
2
C
1
T
T
R
1
q
1
R
2
d
>>
R
1
Problemi
103
V
0
C
1
C
2
C
3
C
4
Q
P
















