
102
C A P I T O L O 4
Conduttori. Dielettrici. Energia elettrostatica
collegati con un sottile filo conduttore. Una carica
q
=
10
–10
C è posta al centro del sistema e una carica
q
0
=
q
è
posta in un punto
B
distante
d
= 25 cm dal foglio esterno.
Calcolare la forza
F
esercitata da
q
0
su ciascun foglio.
4.10
Cinque fogli metallici, sferici di spessore trascurabile,
tutti concentrici, aventi raggi pari rispettivamente a 1, 2,
3, 4 e 5 cm, sono collegati con sottili fili conduttori come
in figura. Il sistema è inizialmente scarico. Una carica
q
=
10
–10
C è depositata sulla superficie più interna. Calco-
lare: a) le cariche
q
1
,
q
2
,
q
3
,
q
4
e
q
5
presenti su ciascuna su-
perficie, b) il campo elettrostatico
E
(
r
) in funzione della
distanza
r
dal centro
O
del sistema e c) l’energia elettro-
statica
U
e
del sistema. Determinare inoltre come variano il
campo elettrostatico
E
(
r
) e l’energia elettrostatica
U
e
quando: d) la sfera 1 è posta in contatto con la sfera 2, e)
la sfera 3 è posta in contatto con la sfera 4, f) la sfera 5 è
collegata a terra.
4.12
Un elettrone di energia cinetica
E
e
= 100 eV è lanciato
verso una lastra metallica indefinita , carica con una den-
sità di carica uniforme
σ
= –1.776 · 10
–6
C/m
2
. Calcolare:
a) da quale distanza
h
dalla lastra deve essere lanciato
l’elettrone per raggiungere la lastra con velocità nulla e
b) a quale distanza
h
dalla lastra arriva un protone lan-
ciato dalla superficie della lastra, con energia cinetica
E
p
= 100 eV.
4.13
Due conduttori sferici
C
1
e
C
2
, cavi, molto sottili, concentrici,
di raggi rispettivamente
R
1
= 10 cm e
R
2
= 20 cm sono soste-
nuti ciascuno da un supporto isolante. La carica
q
1
= –2 ·
10
–8
8
C viene trasferita a
C
1
, la carica
q
2
= 5 · 10
–8
C a
C
2
. Calco-
lare: a) la differenza di potenziale
Δ
V
tra
C
1
e
C
2
. Un con-
duttore sferico
C
3
di raggio
R
3
= 5 cm, sospeso ad un sup-
porto isolante, molto lontano, viene posto in contatto con
C
2
tramite un filo conduttore. Calcolare: b) il potenziale
V
ri-
spetto all’infinito (
V
•
= 0) di
C
2
e
C
3
, c) il campoelettrostatico
E
2
e
E
3
rispettivamente sulla superfice di
C
2
e
C
3
e d) la varia-
zione di energia elettrostatica
Δ
U
e
avvenuta con il contatto.
4.14
Una lastra di rame di spessore
b
= 0.3 cm viene introdotta
parallelamente tra le armature di un condensatore piano
di capacità
C
0
= 100 nF e distanza tra le armature
h
= 0.5
cm, collegato ad un generatore che mantiene una diffe-
renza di potenzale
V
0
= 12V tra le armature stesse. Cal-
colare: a) la capacità
C
dopo l’introduzione della lastra,
b) il campo elettrico
E
nelle parti vuote e c) la variazione
della carica
D
q
fornita dal generatore.
4.15
Un condensatore piano, armature di area
Σ
= 400 cm
2
di-
stanti
d
= 0.5 cm, viene caricato alla differenza di poten-
ziale tra le armature
V
= 50 V e quindi isolato. Le armature
vengono allontanate finché la loro distanza è 2
d
= 1 cm.
Calcolare: a) la differenza di potenziale
V
tra le armature,
b) il campo elettrico
E
prima e
E
dopo l’allontanamento,
c) l’energia elettrostatica del sistema iniziale
U
e
e finale
U
e
e d) il lavoro
W
fatto per allontanare le armature.
4.16
Tre condensatori di capacità
C
1
= 2
μ
F,
C
2
= 2
μ
F e
C
3
= 4
μ
F sono collegati come in figura. La differenza di poten-
ziale applicata tra
A
e
B
è
V
= 100 V. Calcolare: a) la capa-
cità equivalente
C
eq
del sistema tra
A
e
B
, b) la carica
q
i
, c)
la differenza di potenziale
V
i
per ciascun condensatore e
d) l’energia elettrostatica
U
e
del sistema.
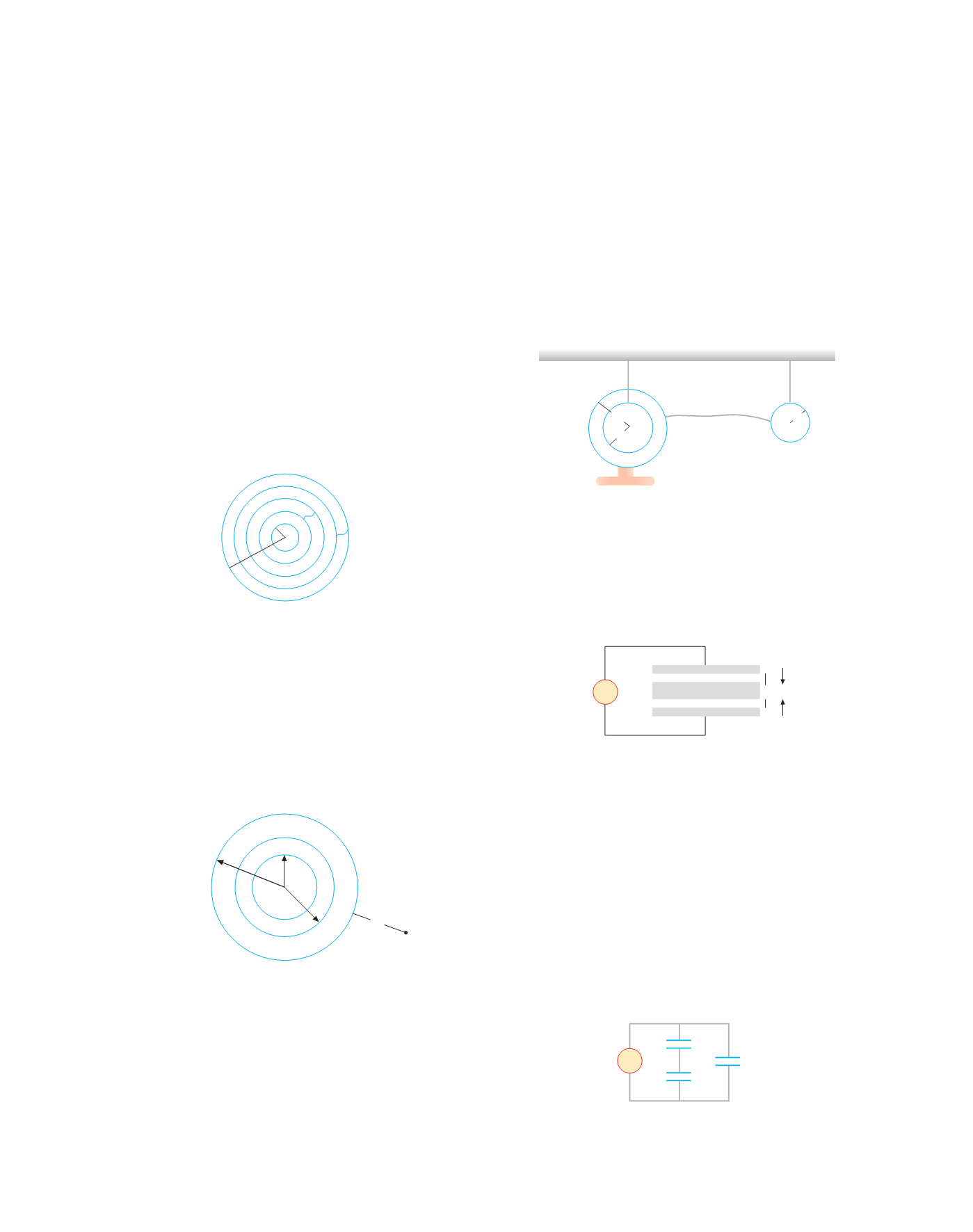
4.11
Tre conduttori
C
1
,
C
2
,
C
3
, sferici, cavi, concentrici, molto
sottili, hanno rispettivamente raggi
R
1
= 5 cm,
R
2
= 10 cm,
R
3
= 20 cm. Una carica positiva
q
1
= 0.5 · 10
–8
C viene tra-
sferita a
C
1
, una carica negativa
q
2
= –4.5 · 10
–8
C a
C
2
e una
carica positiva
q
3
= +6 · 10
–8
C a
C
3
. Calcolare: a) il campo
elettrostatico
E
P
in un punto
P
distante
d
= 30 cm dalla su-
perficie di
C
3
; b) la differenza di potenziale
V
3
–
V
1
tra i
conduttori
C
3
e
C
1
. I due conduttori
C
1
e
C
2
vengono col-
legati con un filo conduttore. Calcolare: c) la variazione
di energia elettrostatica
Δ
U
e
.
R
5
R
1
1
2
3
4
5
V
R
1
R
2
R
3
C
1
C
2
C
3
V
0
b h
B
A
C
2
C
3
C
1
R
1
P
R
3
C
3
d
C
1
C
2
R
2
















