
104
C A P I T O L O 4
Conduttori. Dielettrici. Energia elettrostatica
4.27
Due gocce di mercurio identiche hanno ciascuna carica
q
= 10
–10
C e potenziale
V
= 500 V. Calcolare: a) il raggio
R
delle due gocce. Le due gocce si fondono insieme per for-
mare un’unica goccia. Calcolare: b) il raggio
R
della
nuova goccia e c) il potenziale
V
della stessa.
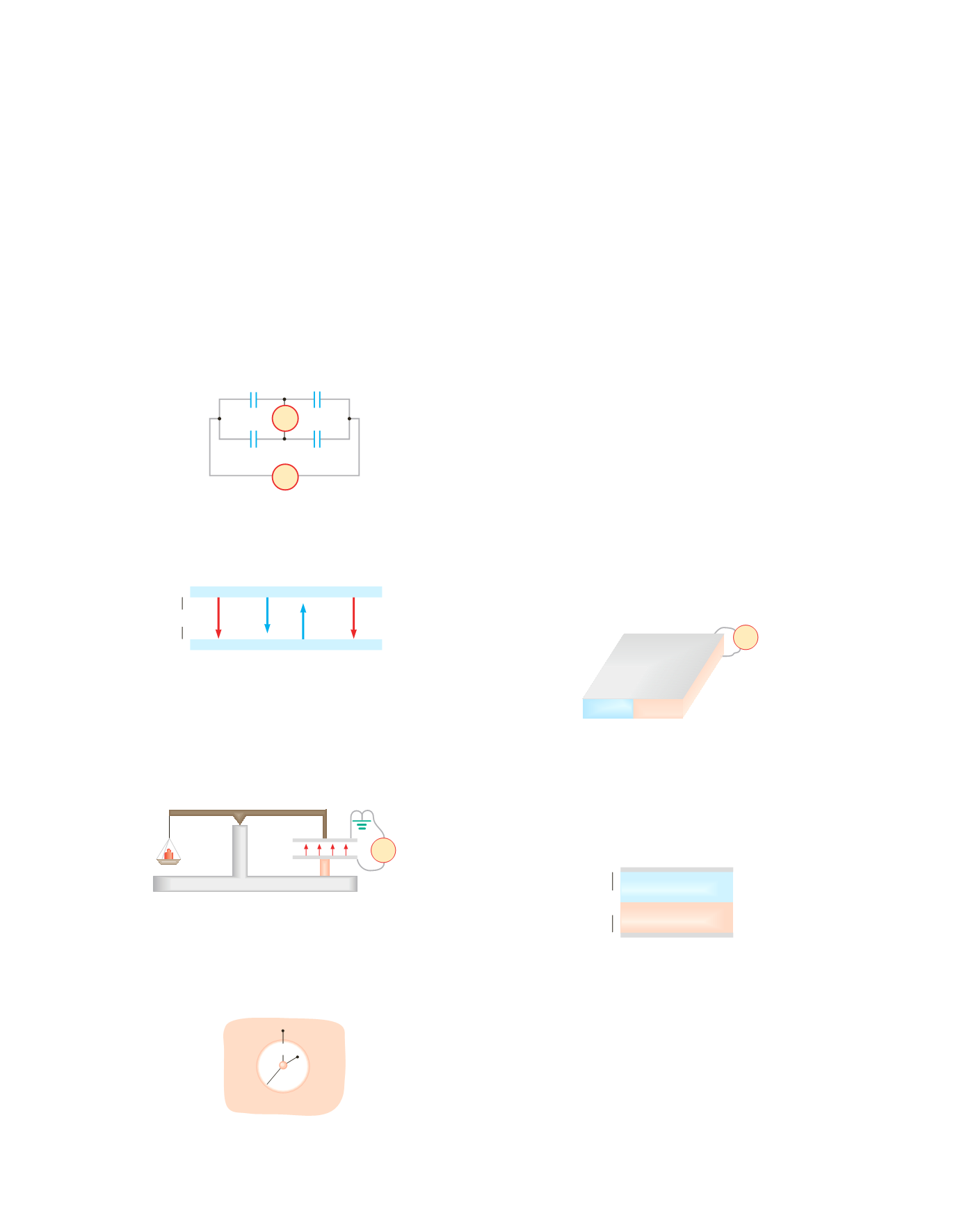
4.28
Quattro condensatori sono disposti come in figura. Un
generatore è collegato tra i punti
A
e
B
e un elettroscopio
(
E
) tra i punti
C
e
D
per misurare la differenza di poten-
ziale
V
C
–
V
D
. Dimostrare che l’elettroscopio segna zero
quando
C
1
/
C
2
=
C
3
/
C
4
(questa disposizione, nota come
ponte capacitivo
, permette di misurare la capacità di un
condensatore note le altre tre).
4.32
Due lastre di alluminio di area
Σ
= 10
3
cm
2
sono separate
da un foglio di carta di spessore
d
. Calcolare la massima
carica
q
s
con cui si possono caricare le due piastre. La
carta ha
κ
= 3.7 e la rigidità dielettrica è
E
s
= 16 · 10
6
V/m.
4.33
Un cavo sottomarino ha un conduttore interno di diame-
tro
d
1
= 2 cm circondato da uno schermo conduttore di
diametro interno
d
2
= 4 cm; tra i conduttori c’è teflon,
κ
=
2.2. Per un cavo lungo
L
= 1 km, calcolare: a) la capacità
C
del cavo e b) l’energia elettrostatica
U
e
immagazzinata,
quando la differenza di potenziale tra i conduttori è
V
=
20 kV.
4.34
Un condensatore piano, armature circolari di raggio
R
=
20 cm distanti
d
= 0.5 cm, è collegato ad un generatore
con
V
0
= 100 V. Lo spazio tra le armature viene completa-
mente riempito con una lastra isolante, di costante die-
lettrica relativa
κ
e
= 2.5. Calcolare: a) la variazione di ener-
gia elettrostatica
D
U
e
, b) il valore del campo elettrico
E
e
c) il valore del vettore polarizzazione
P
.
4.35
Un condensatore piano, con armature quadrate di area
Σ
= 400 cm
2
distanti
d
= 2 mm, è riempito per metà di mica
(
κ
1
= 5) e per metà di paraffina (
κ
2
= 2), come mostrato in
figura. Calcolare: a) la capacità
C
del condensatore. Se tra
le armature viene applicata una differenza di potenziale
V
= 2 · 10
3
V, calcolare: b) il campo elettrostatico
E
, c) la ca-
rica
q
e d) l’energia elettrostatica
U
e
del sistema.
4.29
Tra le armature piane di un condensatore, di area
Σ
e di-
stanti
x
, c’è un campo elettrico
E
. Scrivere: a) l’espres-
sione dell’energia elettrostatica
U
e
(
x
) e b) calcolare la
forza
F
e
tra le armature.
4.30
Nell’
elettrometro a bilancia di Thomson
l’area delle arma-
ture, costituite da due piastre circolari parallale, è
Σ
=
400 cm
2
e la loro distanza è
h
= 5 mm. Connettendo le pia-
stre ad un generatore che mantiene una differenza di po-
tenziale
V
tra le armature, per rimettere la bilancia in
equilibrio occorre aggiungere una massa
m
= 20 mg sul
piatto della bilancia. Calcolare
V
(utilizzando il risultato
del problema 4.29).
4.36
Un condensatore piano, armature quadrate di area
Σ
=
400 cm
2
distanti
d
= 5 mm, è riempito per metà di mica
(
κ
1
= 5) e per metà di paraffina (
κ
2
= 2), come mostrato in
figura. Calcolare: a) la capacità
C
del condensatore. Se la
differenza di potenziale applicata è
V
= 2 · 10
3
V, calco-
lare: b) la carica
q
sulle armature e c) l’energia elettrosta-
tica
U
e
immagazzinata.
4.37
Le armature del condensatore del problema 4.36, hanno
una carica
q
= 4 · 10
–7
C. Calcolare: a) la carica di polariz-
zazione
q
P
1
presente sulla superficie della lastra di mica e
la carica di polarizzazione
q
P
2
su quella di paraffina a con-
tatto con le armature del condensatore e b) la carica di
polarizzazione
q
P
presente sulla superficie di contatto
mica-paraffina.
4.38
Una sfera conduttrice di raggio
R
= 1 cm, è circondata da
un guscio di materiale isolante di spessore
d
e possiede una
4.31
Una carica
q
= 2 · 10
–8
C è posta al centro di una cavità sfe-
rica di raggio
R
= 2 cm, praticata all’interno di un blocco
di materiale isolante, avente costante dielettrica relativa
κ
= 2.5. Calcolare: a) il campo elettrico
E
1
in un punto
P
1
di-
stante
r
1
= 1 cm dalla carica e b) il campo elettrico
E
2
in un
punto
P
2
, distante
r
2
= 3 cm dalla carica stessa.
_
+
E
V
_ _ _ _ _ _ _
+ + + + + + +
V
V
A
B
C
D
C
1
C
2
C
3
C
4
F
e
E
E
x
κ
1
κ
2
d
κ
1
κ
2
+
P
2
P
1
r
1
r
2
R
















