
94
C A P I T O L O 4
Conduttori. Dielettrici. Energia elettrostatica
d
p
=
P
d
τ
=
P d
Σ
0
d
h
,
essendo
d
h
orientato concordemente a
P
.
Sostituiamo al prisma un sistema costituito da due cariche ±
dq
p
= ±
Pd
Σ
0
, poste
nel
vuoto
e distanti
dh
, distribuite sulle basi del prisma con
densità
±
σ
p
= ±
dq
p
/
d
Σ
0
=
±
P
.
Tali cariche hanno un momento di dipolo d
p
eguale a quello del prisma
.
Se consideriamo due prismi consecutivi, figura 4.43b, con una base in comune
e se
P
è costante, la carica +
dq
p
di un prisma si annulla con la carica –
dq
p
dell’altro
sulla base in comune; ripetendo l’operazione per tutti i prismi alla fine rimangono
solamente le cariche sulle basi dei prismi che appartengono alle facce della lastra,
figura 4.43c.
Il significato fisico dell’operazione è di ammettere che avvenga una compensa-
zione delle cariche, spostate dalle posizioni di equilibrio, all’interno del dielettrico
uniformemente polarizzato, ma
non
alla superficie limite dove la discontinuità del
mezzo impedisce la compensazione. Qui la
carica
è
localizzata
entro uno strato di
spessore pari alle dimensioni atomiche ed è a tutti gli effetti trattabile come una di-
stribuzione superficiale di carica. La
lastra
viene quindi ad essere
equivalente a due
distribuzioni di carica, localizzate sulle facce, con densità
±
σ
p
= ±
P
.
È bene ripetere che queste
cariche di polarizzazione non sono libere
come nei con-
duttori: esse si manifestano a causa degli
spostamenti microscopici locali, ma rimangono
vincolate agli atomi
. Per questo motivo quando cerchiamo di prelevarne un cam-
pione non riusciamo ad asportarne nemmeno una piccola quantità misurabile.
Per lo stesso motivo quando un dielettrico occupa completamente lo spazio in-
terno a un condensatore e le facce del dielettrico vengono in più punti a contatto
con le cariche libere presenti sulle armature conduttrici non avvengono trasferi-
menti di carica, pur essendo affacciate cariche di segno opposto.
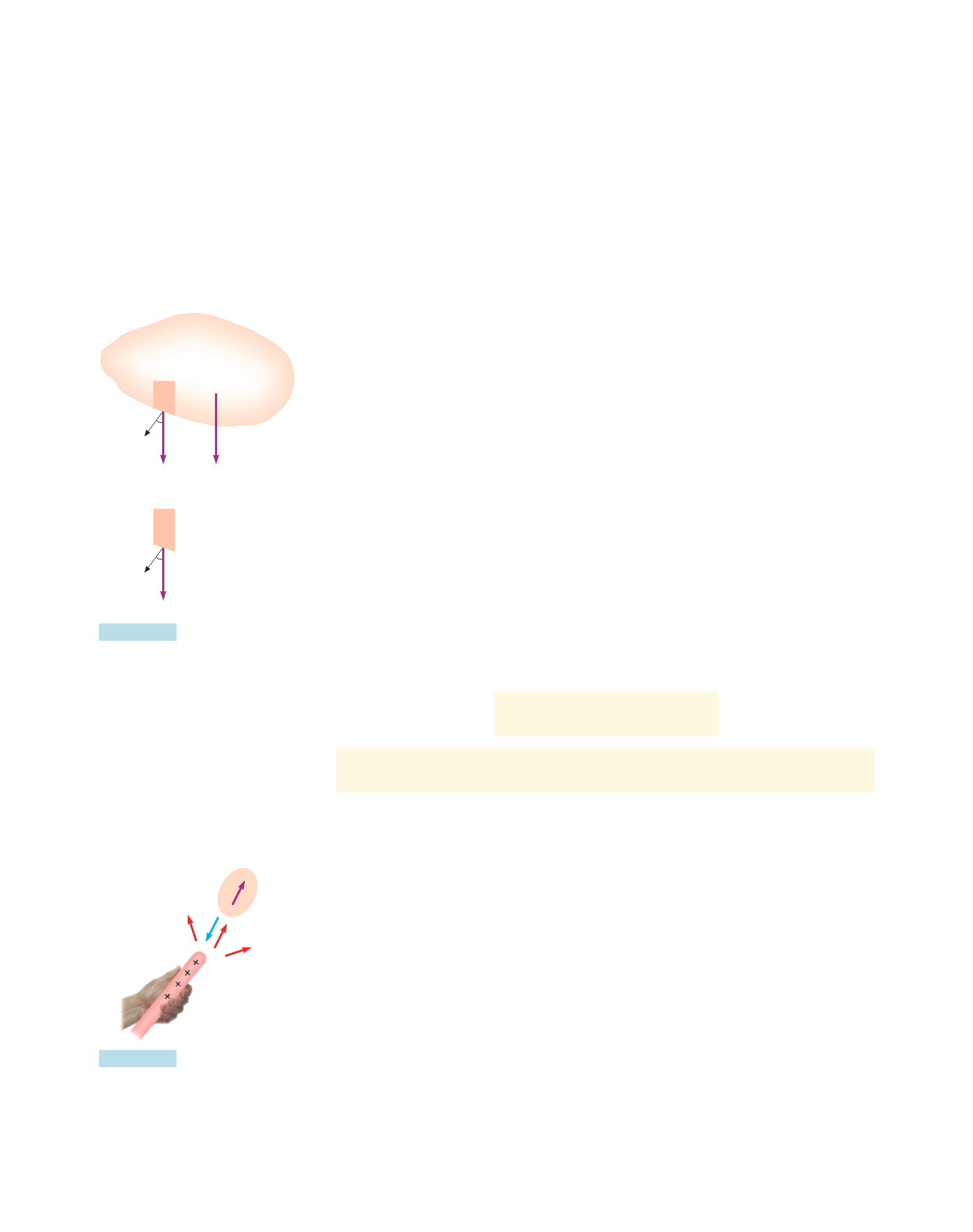
Quando la superficie del dielettrico, come in figura (4.44), è di forma qualun-
que, considerato un prismetto con le basi una interna di area
d
Σ
0
in cui la densità
di carica è ancora
P
e l’altra esterna di area
d
Σ
in cui la densità è
σ
p
si ha
dq
p
=
Pd
Σ
0
=
σ
p
d
Σ
e quindi:
d
Σ
0
σ
p
=
P
––– =
P
cos
θ
=
P
·
u
n
:
(4.36)
d
Σ
la densità superficiale delle cariche di polarizzazione è uguale alla compo-
nente di
P
lungo la normale alla superficie.
Il caso della lastra considerata in precedenza corrisponde alle due orienta-
zioni particolari
θ
= 0 e
θ
=
π
. In generale, figura 4.44, quando 0
£
θ
<
π
/2 la
densità di carica è positiva, quando
π
/2 <
θ
£
π
essa è negativa ed è nulla solo
per
θ
=
π
/2, superficie parallela a
P
. Di conseguenza in un dielettrico polariz-
zato, indipendentemente dalla forma, avremo
sempre
una parte della superficie
carica positivamente e la rimanente carica negativamente. Se la
polarizzazione
è
uniforme
non si manifestano cariche all’interno del dielettrico e quindi la
carica
totale superficiale deve essere nulla
, come deve sempre essere una carica di pola-
rizzazione visti i meccanismi da cui ha origine. Se invece la polarizzazione non
è uniforme diciamo soltanto che pure all’interno del dielettrico si hanno cari-
che di polarizzazione, in quanto non si ha più la compensazione cui si è ac-
cennato prima. Però la somma delle cariche di polarizzazione superficiali e di
volume è sempre nulla.
L’attrazione di piccoli oggetti isolanti, per esempio pezzetti di carta o di poli-
stirolo, da parte di corpi carichi, come materiali dielettrici strofinati, si spiega con
il fenomeno della polarizzazione: il campo elettrostatico del corpo carico polarizza
l’oggetto che acquista un momento di dipolo elettrico
p
e il segno delle cariche è
+++
+
+
++++++++
++
+
+
+
–
–
– – – – – – – – – – – – –
–
–
–
– –
u
n
P
P
P
+
dq
p
–
dq
p
d
Σ
d
Σ
0
θ
θ
+
+
+
+
– –
–
–
–
E
F
P
r
Un pezzetto di polistirolo viene
attratto da una bacchetta elet-
trizzata.
Figura 4.44
Figura 4.45
Densità di carica di polarizzazio-
ne sulla superficie di un dielet-
trico di forma qualunque.
















