
Le configurazioni regolari del campo
E
, considerate nel condensatore cilin-
drico e nel condensatore piano, non sono completamente realizzabili nella pra-
tica. Esse sarebbero corrette se l’estensione fosse indefinita; per una dimensione fi-
nita si avrebbe, nella zona del bordo, un passaggio brusco dalla regione in cui esi-
ste un campo elettrico regolare alla regione con campo elettrico nullo e sarebbe
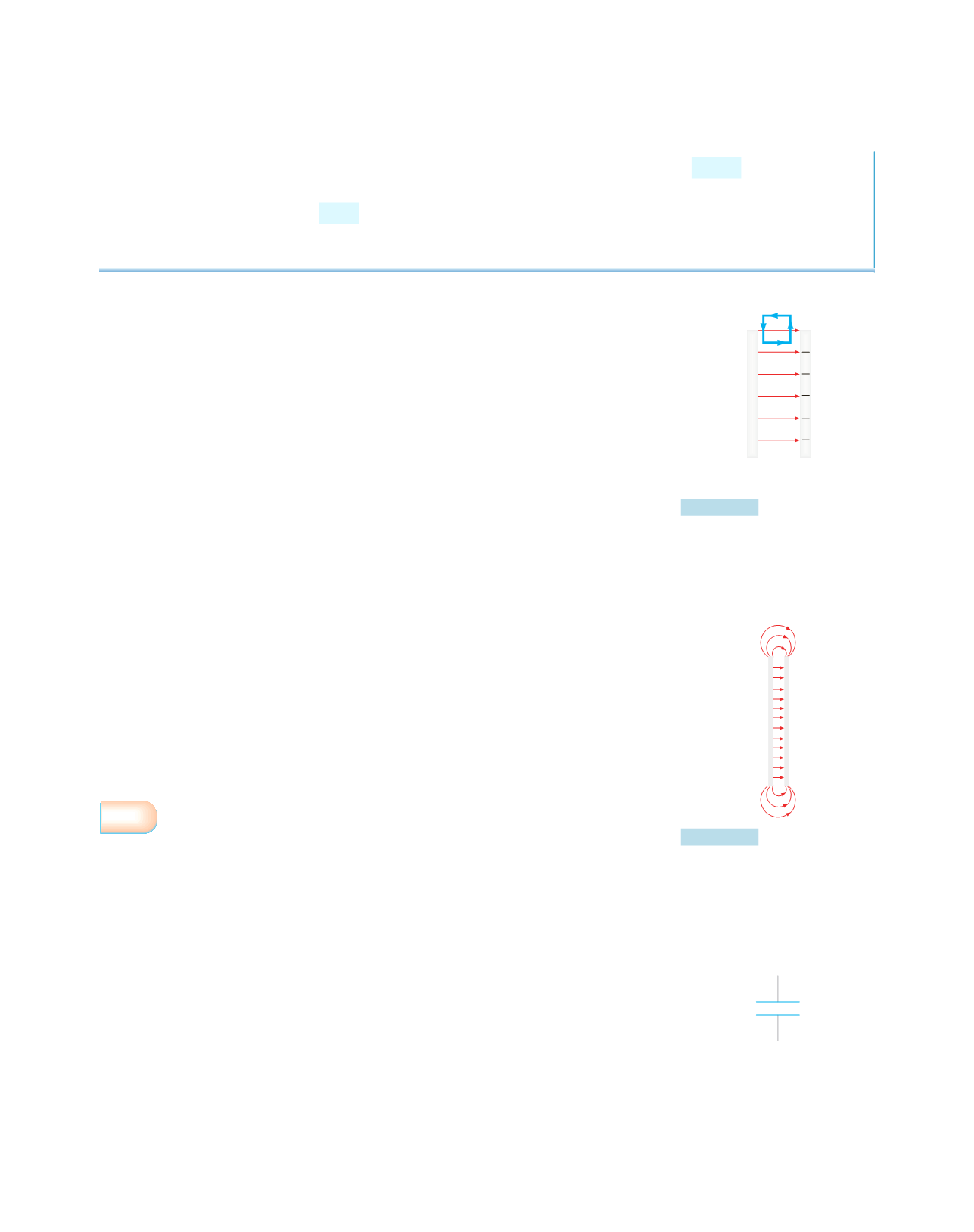
possibile trovare una linea chiusa, come quella mostrata in figura 4.21, tale che
E
·
d
s
π
0 .
Essendo il campo elettrostatico conservativo, questa possibilità va esclusa e in ef-
fetti il campo
E
è regolare solo nella zona centrale del condensatore, mentre vi-
cino ai bordi le linee di forza sono deformate ed escono all’esterno, assumendo
una configurazione che assicura la nullità della circuitazione del campo elettrosta-
tico; il valore del campo è ad ogni modo rapidamente decrescente verso l’esterno,
figura 4.22.
D’altra parte sono dovuti alla presenza del
campo elettrostatico disperso
alcuni
effetti fisici osservati, quali ad esempio il risucchio di una lastra di isolante all’in-
terno di un condensatore piano, mostrato nella figura 4.38 dell’esempio 4.13.
Si capisce che la configurazione sferica sarebbe l’unica ideale, per l’assenza dei
bordi. Le capacità reali di condensatori cilindrici e piani differiscono dal valore cal-
colabile con le espressioni (4.9) e (4.12). Tuttavia queste vengono sempre usate per
avere un’indicazione dei valori in gioco, tanto più vicina alla situazione reale quanto
più ci si pone nella condizione
Σ
>>
h
2
(dimensioni delle armature grandi rispetto
alla loro distanza) per la quale l’effetto di bordo è sostanzialmente trascurabile.
COLLEGAMENTO DI CONDENSATORI
Un condensatore viene utilizzato essenzialmente come deposito di carica; pur
essendo la carica totale nulla, essa è separata nella quantità +
q
e –
q
, proporzionali
per un conduttore di data capacità alla differenza di potenziale tra le armature.
Tramite opportuni collegamenti conduttivi esterni è possibile far fluire la carica
negativa (elettroni) da un’armatura all’altra, generando una corrente elettrica
che scarica il condensatore. Vedremo questo argomento nel capitolo 5. Possiamo
però subito descrivere come si collegano con fili conduttori più condensatori tra
loro e calcolare la capacità equivalente. Noi supponiamo costanti nel tempo le ca-
riche e le differenze di potenziale, però i risultati sono validi anche in regime va-
riabile.
Per comodità scriviamo
V
la differenza di potenziale
V
1
–
V
2
che esiste tra le ar-
mature; inoltre con la lettera
C
indichiamo sia il condensatore che la sua capacità.
Nella figura a fianco è mostrato il
simbolo
che individua un
condensatore
in un cir-
cuito elettrico: esso si rifà chiaramente al condensatore piano, che è la configura-
zione di gran lunga più comune, però è valido per qualsiasi condensatore.
Per il calcolo della capacità del condensatore sferico utiliz-
ziamo la (4.8) in quanto
h
/
R
terra
ª
7.8 · 10
–4
:
4
π
R
2
terra
C
=
ε
0
––––––– = 0.9 F .
h
La differenza di potenziale è quindi:
q
Δ
V
= ––
ª
500 kV ,
C
peraltro deducibile direttamente da
Δ
V
=
Eh
= 500 kV, poiché
l’uso di
C
=
ε
0
g
/
h
implica che il campo elettrostatico sia co-
stante.
+
+
+
+
+
E
·
d
s
π
0
4.4
C
4.4 Collegamento di condensatori
79
Dimostrazione dell’esistenza del
campo elettrostatico disperso sui
bordi di un condensatore piano
di dimensioni finite.
Figura 4.21
Linee di forza di un condensa-
tore piano.
Figura 4.22
Simbolo del condensatore
















