
82
C A P I T O L O 4
Conduttori. Dielettrici. Energia elettrostatica
ENERGIA DEL CAMPO ELETTROSTATICO
Il
processo di carica
di un condensatore, in cui si passa dalla situazione di carica zero
sulle armature alla situazione (+
q
, –
q
) con una differenza di potenziale
V
=
q
/
C
tra le
armature, consiste in definitiva in una
separazione di cariche
e richiede un determi-
nato lavoro che, essendo il campo elettrostatico conservativo, dipende soltanto dallo
stato iniziale e dallo stato finale, ma non dalle modalità con cui avviene il processo.
Per eseguire il calcolo possiamo immaginare quindi che la carica di un condensatore
avvenga sottraendo, tramite un agente esterno, una carica
dq
dall’armatura negativa
e portandola sull’armatura positiva, così che alla fine una carica +
q
è stata trasferita
da un’armatura all’altra, lasciando la prima con una carica –
q
, e si è stabilita tra le ar-
mature la differenza di potenziale
V
;
la carica totale è in ogni istante nulla
.
Se in una fase intermedia del processo la differenza di potenziale tra le arma-
ture è
V
, in quanto è già stata trasferita la carica
q
=
C V
il lavoro per spostare
l’ulteriore carica
dq
attraverso la differenza di potenziale
V
è, secondo (2.8),
q
dW
=
V dq
= ––
dq
C
e quindi il lavoro complessivo per effettuare la separazione delle cariche è
q
q
2
W
=
∫
dW
=
∫
q
0
––
dq
= ––– .
C
2
C
Come si vede, esso dipende solo dalla carica trasportata e dalla capacità del con-
densatore e non contiene informazioni sul processo effettivo.
Questo lavoro, effettuato contro la forza elettrostatica che si oppone a un ac-
cumulo di cariche dello stesso segno, viene immagazzinato nel sistema sotto forma
di
energia
(potenziale)
elettrostatica
. Assumendo che l’energia sia nulla quando
q
= 0, abbiamo
W
=
U
e
e, servendoci delle (4.6), scriviamo tre espressioni equiva-
lenti per l’energia elettrostatica del condensatore di capacità
C
, carico con carica
q
e differenza di potenziale
V
:
1
q
2
1
1
U
e
= –– ––– = ––
CV
2
= ––
qV
.
(4.17)
2
C
2
2
4.5
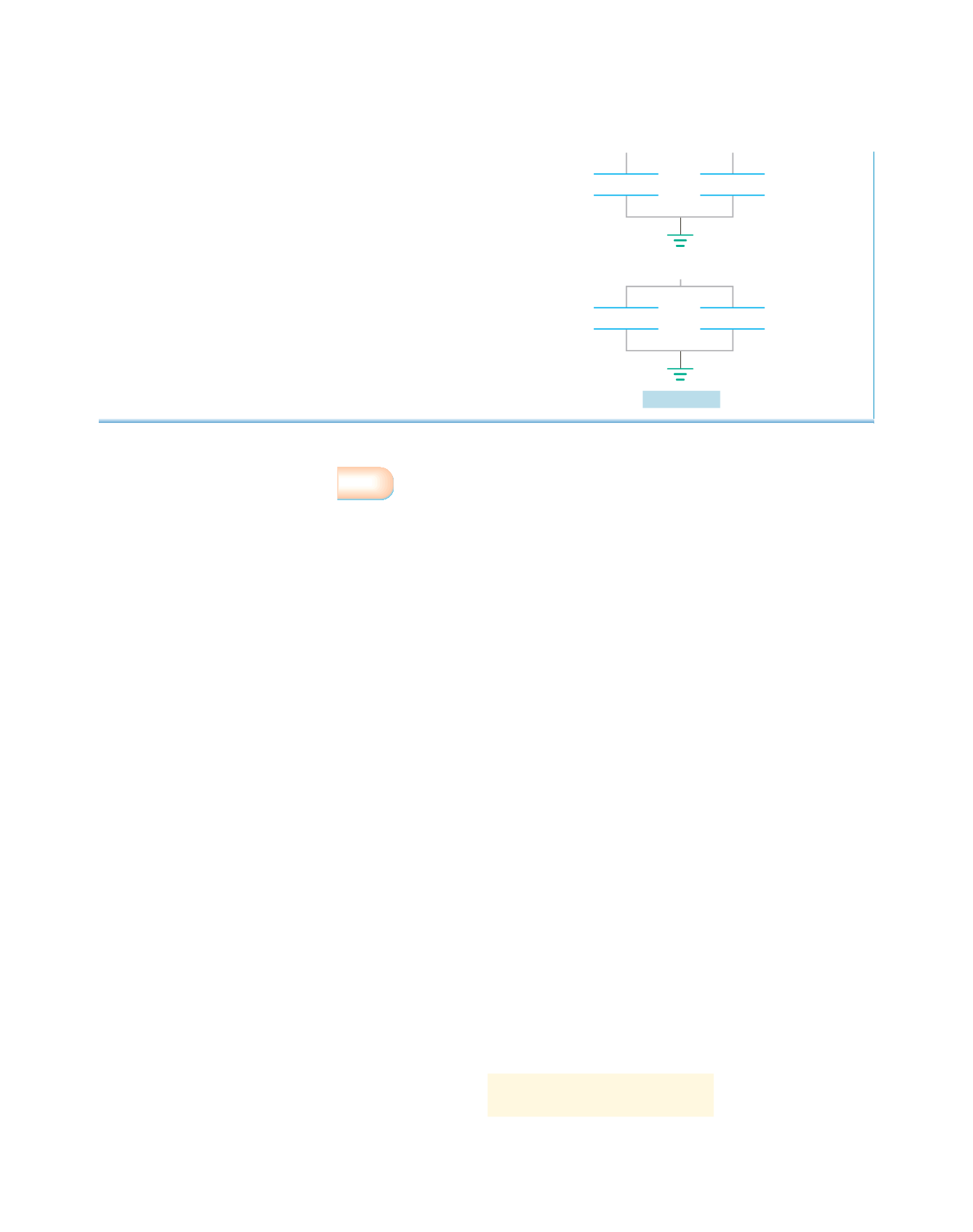
L’equilibrio viene raggiunto con un passaggio di carica po-
sitiva dall’armatura a potenziale maggiore a quella a poten-
ziale minore e le cariche finali dei condensatori sono
C
1
C
2
q
1
=
C
1
V
= –––––––
q
,
q
2
=
C
2
V
= –––––––
q
.
C
1
+
C
2
C
1
+
C
2
Si osservi che la ripartizione di carica tra i due condensa-
tori avviene nello stesso modo dell’esempio 4.1, relativo a due
sfere conduttrici messe in contatto, se si ricorda l’espressione
(4.7) della capacità di un conduttore sferico isolato.
V
1
V
2
V
C
1
C
2
C
1
C
2
Energia elettrostatica
Figura 4.26
















