
78
C A P I T O L O 4
Conduttori. Dielettrici. Energia elettrostatica
con
Σ
= 2
π
R d
area delle armature distanti
h
: si ritrova la (4.8).
Dalla (4.9) si definisce la
capacità per unità di lunghezza
C
2
π ε
0
C
d
= –– = ––––– .
(4.11)
d
R
2
ln –––
R
1
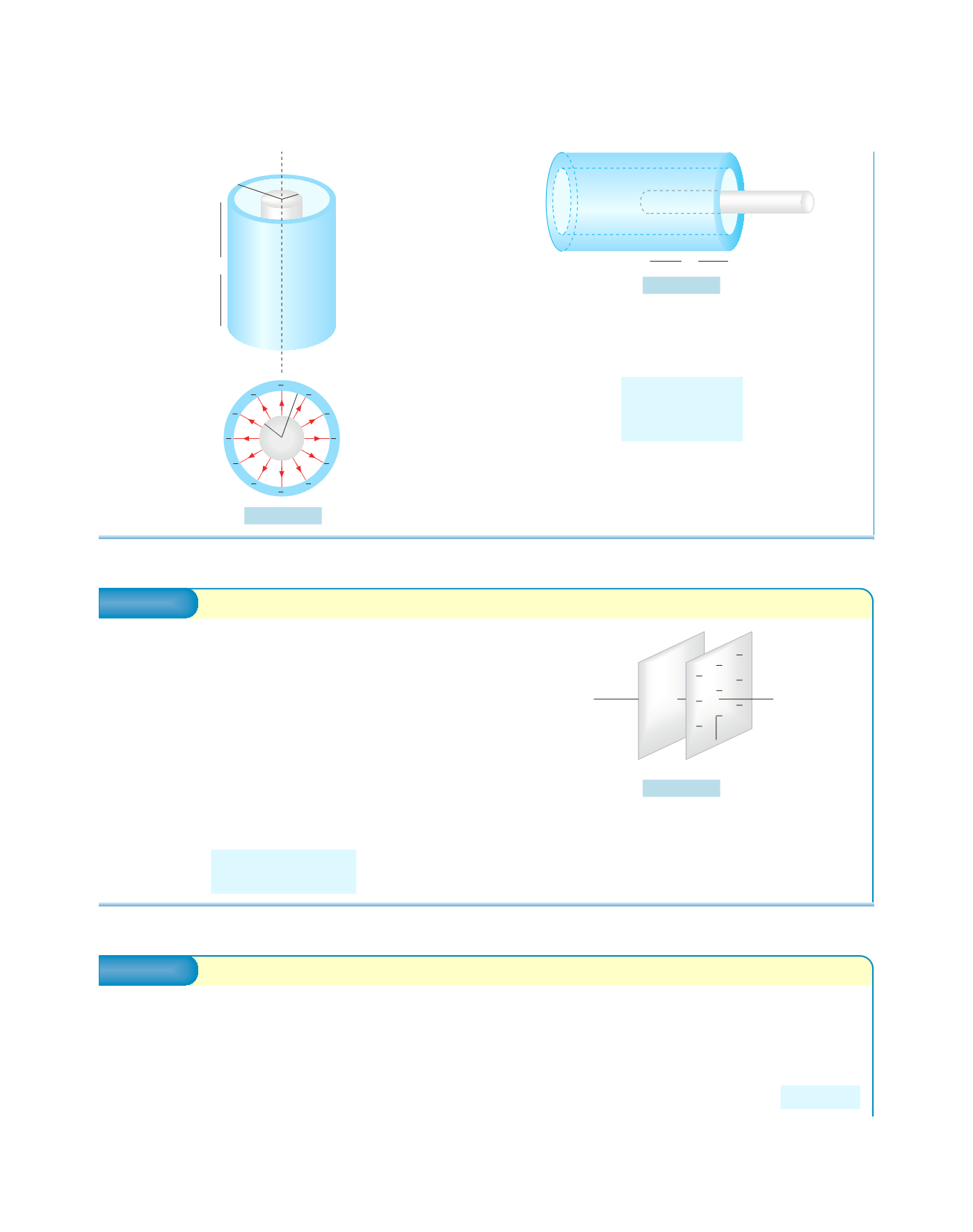
Si realizza un condensatore cilindrico a capacità variabile
facendo scorrere uno dei due cilindri lungo l’asse in modo da
far variare la lunghezza
d
. Le formule restano valide se si pos-
sono trascurare gli effetti di bordo.
+ +
+
+
+
++
+
+
+
R
2
R
1
R
1
R
2
d
d
Le armature di un condensatore piano sono costituite da
due conduttori piani paralleli, di area
Σ
e distanti
h
, figura
4.20. La carica positiva
q
è distribuita con densità uniforme
σ
sull’armatura positiva e quella negativa –
q
con densità uni-
forme –
σ
sull’armatura negativa. Abbiamo già calcolato campo
e potenziale per una tale distribuzione di cariche negli esempi
1.8 e 2.8, supponendo la struttura indefinita:
σ
σ
σΣ
q
E
= ––
u
n
,
V
1
–
V
2
=
E h
= ––
h
= ––––
h
= ––––
h
.
ε
0
ε
0
ε
0
Σ
ε
0
Σ
Si deduce quindi che la capacità di un condensatore piano
è data da
q
ε
0
Σ
C
= ––––––– = –––– ,
(4.12)
V
1
–
V
2
h
coincidente con (4.8) e (4.11). Questa volta non ci sono ap-
prossimazioni geometriche, però la (4.12) è approssimata per
un’altra ragione: il campo si può supporre uniforme solo nella
regione centrale del condensatore, lontano dai bordi.
E
SEMPIO
4.4
Capacità di un condensatore piano
Il campo elettrostatico in condizioni di bel tempo sulla su-
perficie terrestre è in media
E
terra
ª
100 V/m, diretto verso la
terra. Un modello fenomenologico per spiegare l’origine di
questo campo elettrostatico consiste nel pensare la superficie
terrestre come l’armatura inferiore di un condensatore sferico
carico negativamente in cui l’altra armatura, consistente in
una distribuzione di carica positiva, si trova a circa
h
= 5 km di
distanza dalla superficie della terra. Calcolare la capacità
C
del
condensatore e la carica
q
presente sulle armature.
Soluzione
La densità di carica e la carica presenti sulla terra
si ricavano dal teorema di Coulomb (4.1):
C
σ
= –
ε
0
E
terra
= –8.86 · 10
–10
––– ,
q
= –
σ
4
π
R
2
terra
= –4.56 · 10
5
C .
m
2
E
SEMPIO
4.5
Il campo elettrico dell’atmosfera terrestre
+
+
+
+
+
+
h
+
q
–
q
Σ
Figura 4.18
Figura 4.20
Figura 4.19
















