
CONDUTTORE CAVO. SCHERMO ELETTROSTATICO
Consideriamo un conduttore carico che abbia nel suo interno una cavità all’in-
terno della quale non ci siano cariche elettriche, figura 4.8. Nella massa del con-
duttore il campo elettrostatico è nullo e pertanto è nullo il flusso attraverso qual-
siasi superficie chiusa, in particolare attraverso qualsiasi superficie chiusa
Σ
che
racchiuda la cavità: segue, per la legge di Gauss, che all’interno di
Σ
non ci sono
cariche e quindi
sulle pareti della cavità la carica è nulla
.
Non è nemmeno possibile sulle pareti una separazione della carica in +
q
e –
q
:
per negare questa circostanza si ricorre all’altra proprietà fondamentale di
E
,
quella di essere conservativo.
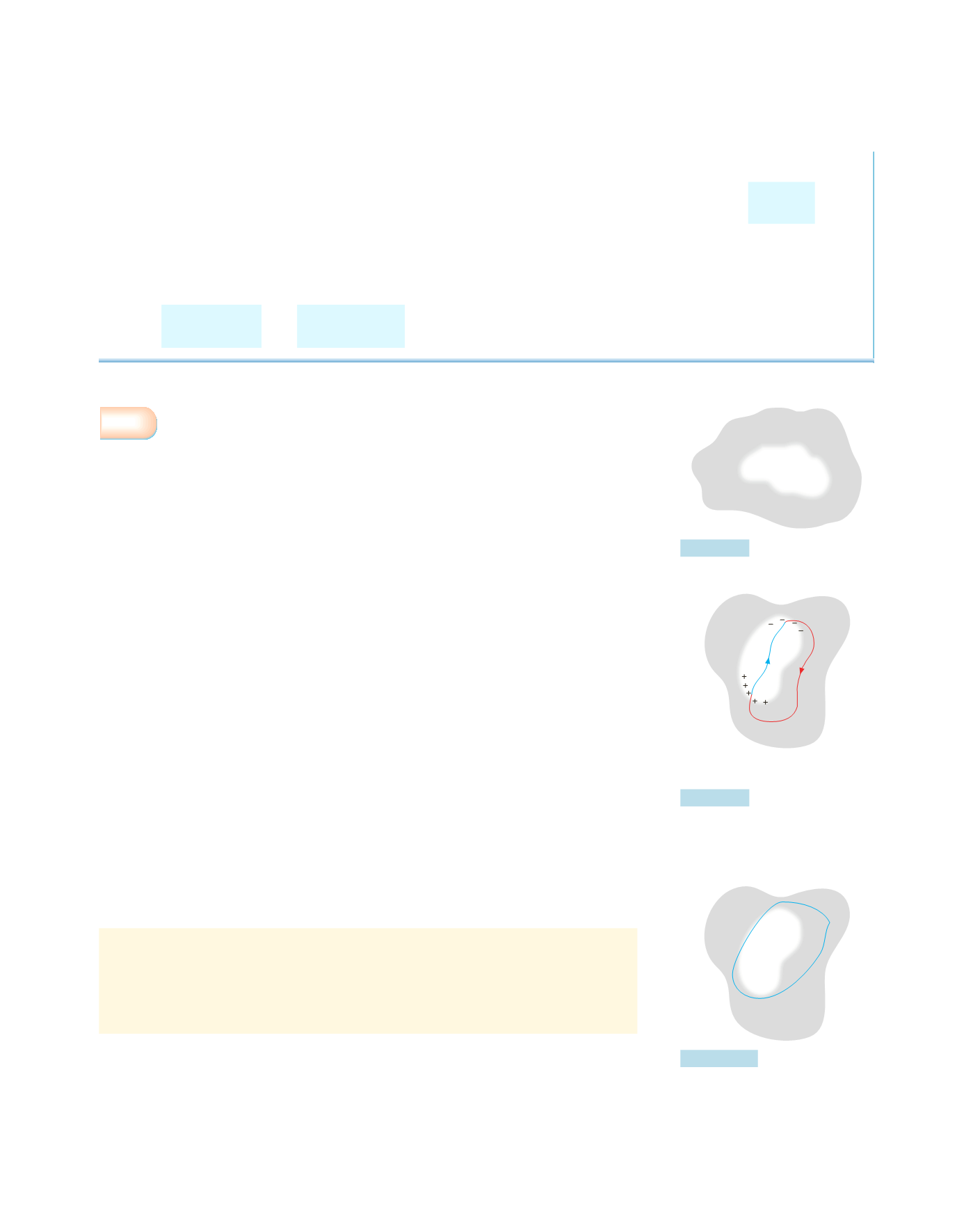
Infatti, se sulle pareti della cavità fossero presenti due distribuzioni di carica di
segno opposto, figura 4.9, ci sarebbero nella cavità linee di forza, uscenti dalle ca-
riche positive e entranti in quelle negative. La circuitazione di
E
lungo una linea
chiusa, costituita da un tratto
C
1
interno alla cavità su cui
E
π
0 e da un tratto
C
2
in-
terno al conduttore dove
E
= 0, darebbe
E
·
d
s
=
∫
C
1
E
·
d
s
+
∫
C
2
E
·
d
s
=
∫
C
1
E
·
d
s
π
0 ,
in contrasto col fatto che
E
è conservativo. Pertanto il campo nella cavità deve es-
sere nullo se l’integrale di linea esteso a
qualsiasi percorso
C
1
interno alla cavità deve
essere nullo:
sulle pareti della cavità non possono esserci cariche elettriche
. Inoltre è
chiaro che il potenziale elettrostatico in un qualsiasi punto della cavità è uguale a
quello del conduttore: se ci fosse una differenza di potenziale dovrebbe infatti es-
serci un campo elettrostatico diverso da zero.
In conclusione:
• la carica di un conduttore in equilibrio elettrostatico si distribuisce sem-
pre e soltanto sulla superficie esterna, anche in presenza di una o più ca-
vità all’interno del conduttore;
• il campo elettrostatico ènullo e il potenziale elettrostatico è costante inogni
punto interno alla superficie del conduttore, anche in presenza di cavità.
In particolare un conduttore sferico isolato carico di raggio
R
, che sia pieno o
con una cavità sferica concentrica o con cavità di qualsiasi forma, ha sempre
campo elettrostatico nullo all’interno e campo elettrostatico in vicinanza della su-
perficie esterna, figura 4.11:
q
1
q
2
––––––– =
V
1
=
V
2
= –––––––
4
π ε
0
R
1
4
π ε
0
R
2
ovvero
q
1
R
1
–– = –– .
(4.2)
q
2
R
2
La carica si ripartisce tra le sfere proporzionalmente ai rag-
gi. Ricordando che
q
=
q
1
+
q
2
abbiamo
R
1
R
2
q
1
=
––––––– q
,
q
2
=
––––––– q
.
R
1
+
R
2
R
1
+
R
2
La densità di carica sulle sfere vale
q
1
q
2
σ
1
R
2
E
1
R
2
σ
1
= ––––– ,
σ
2
= –––––
⇒
–– = –– , –– = –– , (4.3)
4
π
R
2
1
4
π
R
2
2
σ
2
R
1
E
2
R
1
utilizzando il teorema di Coulomb (4.1). Abbiamo verificato in
un caso particolare l’affermazione fatta nel paragrafo 4.1 che
densità di carica e campo elettrico superficiale sono maggiori
dove minore è il raggio di curvatura.
4.2
+
+
+
+
+
+ +++
+
++
+
+
+
+
+
+ + + + +
4.2 Conduttore cavo. Schermo elettrostatico
73
Conduttore cavo carico isolato.
Figura 4.8
Proprietà del campo elettrosta-
tico e del potenziale elettrosta-
tico all’interno di un conduttore
cavo.
Figura 4.9
Applicazione della legge di Gauss
per la verifica dell’assenza di cari-
che sulle pareti di una cavità.
Figura 4.10
E
= 0
E
= 0
V
B
A
C
1
C
2
E
·
d
s
π
0
E
= 0
Σ
















