
74
C A P I T O L O 4
Conduttori. Dielettrici. Energia elettrostatica
σ
q
E
= —
u
n
= –––––––
u
n
(4.4)
ε
0
4
π ε
0
R
2
uguale a quella di una carica puntiforme
q
posta nel centro
O
della superficie sfe-
rica.
Una osservazione importante è la seguente: la situazione descritta all’interno
della cavità di un conduttore cavo non dipende dalla carica e quindi dal potenziale
del conduttore. Il conduttore può essere a 10 V o a 10
6
V, ma all’interno della cavità
non si misura mai tra due punti una differenza di potenziale diversa da zero
: il punto di ri-
ferimento per il potenziale elettrostatico è la parete della cavità, rispetto a cui la dif-
ferenza di potenziale è nulla, qualunque sia il valore del potenziale del conduttore.
Consideriamo adesso un conduttore
C
2
cavo, isolato e privo di carica, e intro-
duciamo un altro conduttore
C
1
carico nella cavità, mantenendolo isolato da
C
2
, fi-
gura 4.12. In condizioni di equilibrio, se
C
1
ha sulla sua superficie esterna una ca-
rica
q
, una carica –
q
risulta distribuita sulla superficie interna e una carica
q
sulla
superficie esterna di
C
2
.
Tale fatto si spiega subito con la legge di Gauss: attraverso una superficie chiusa
Σ
interna a
C
2
e contenente la cavità il flusso di
E
è nullo in quanto è nullo il campo
stesso; di conseguenza all’interno di
Σ
non c’è carica e se
C
1
porta la carica
q
, sulla
superficie interna di
C
2
deve necessariamente comparire una carica –
q
. Inoltre es-
sendo
C
2
neutro, lo spostamento di una carica –
q
sulla superficie interna provoca
la comparsa di una carica +
q
sulla superficie esterna.
Siamo di fronte a un fenomeno di induzione che in questo caso, essendo la ca-
rica
q
completamente contenuta all’interno di una cavità chiusa, si chiama
indu-
zione completa: tutte le linee di forza che partono da
C
1
terminano su
C
2
, figura
4.13. Dalla superficie esterna di
C
2
partono altre linee di forza, il cui andamento in
prossimità del conduttore riflette la distribuzione delle cariche sulla superficie
stessa. Le due zone in cui esiste un campo sono separate da una zona in cui, in
equilibrio, non può esistere campo elettrostatico.
Il campo elettrostatico all’interno della cavità è determinato dal valore di
q
,
dalla posizione di
C
1
e dalla forma geometrica delle due superficie affacciate. Però,
fissato
q
, all’esterno l’effetto è sempre lo stesso, qualunque siano forma e posi-
zione. Infatti possiamo dire che l’
informazione
sulla situazione interna potrebbe
passare all’esterno solo attraverso un campo elettrostatico che penetrasse nel con-
duttore
C
2
: ma questo non è possibile per la proprietà dei conduttori in equilibrio
di avere campo elettrostatico nullo all’interno. Al limite si può portare
C
1
a con-
tatto con
C
2
, con il che le cariche +
q
e –
q
si elidono, ma all’esterno non cambia
nulla: questo fatto, la cui verifica sperimentale vedremo tra breve, ci fa anche ca-
pire che la distribuzione della carica –
q
sulla faccia interna di
C
2
è sempre tale che,
sommando l’effetto della carica
q
di
C
1
, il campo elettrostatico dovuto alle cariche
nella cavità è nullo all’esterno della cavità.
Analogamente, se variamo la carica sulla superficie esterna oppure variamo la
sua distribuzione, ad esempio avvicinando al conduttore un altro corpo carico,
cambia il campo elettrostatico all’esterno, ma la distribuzione di carica sulla su-
perficie esterna di
C
2
è sempre tale da dare campo elettrostatico nullo all’interno
di
C
2
e quindi non può alterare il campo locale esistente nella cavità. Come osser-
vato prima, ciò potrebbe avvenire se un campo elettrostatico penetrasse dal-
l’esterno nella massa del conduttore, ma la possibilità è esclusa dalle proprietà di
un conduttore in equilibrio.
Pertanto finché lo spazio interno e lo spazio esterno non sono comunicanti:
• il conduttore cavo costituisce uno schermo elettrostatico perfetto tra
spazio interno e spazio esterno.
+
+
+
+
+
+
+
+
+ + + + + + + + +
+
+
+
+
+
+
+
+
+
+
++++++++++
+
+
+
+ + + +
+
+++++
– – –
– –
–
–
–
–
–
–
–– – ––
–
–
–
–
–
–
–
–
–
+
+
+
+
+
+
+
+
+ + + + + + + + + + +
+
+
+
+
+
+
+
++++++++++++
+
+
+ ++ +
+
+++++
– – – – –
–
–
–
–
–
–
––––––
–
–
–
–
–
–
– +
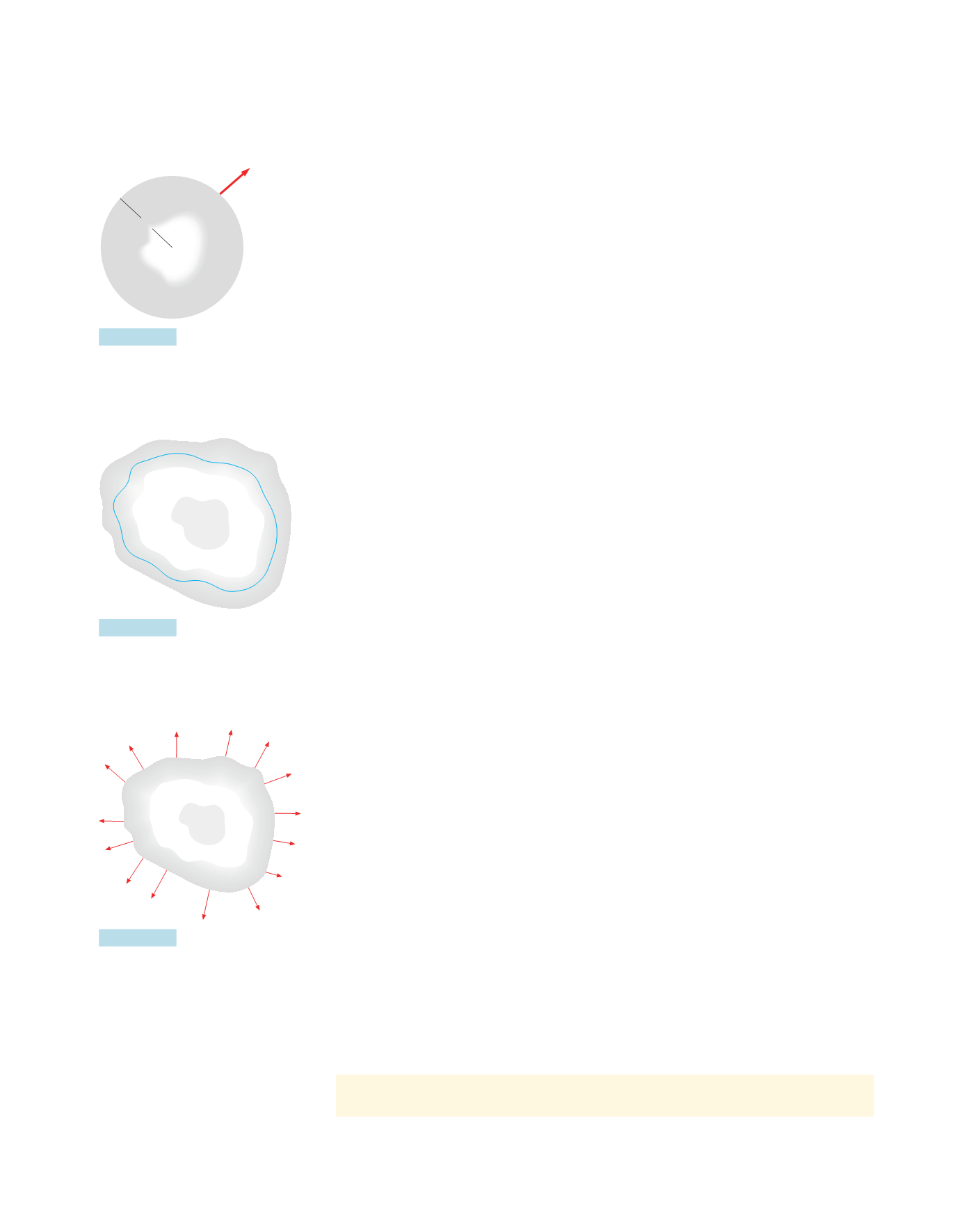
Conduttore cavo carico conte-
nente all’interno un conduttore
isolato carico.
Figura 4.12
Linee di forza di un sistema di
due conduttori in condizione di
induzione elettrostatica completa
.
Figura 4.13
+++
+
+
+
+
+
+
+
+
+
+
+ + + + + + + + +
+
+
+
+
+
+
+
+
+
+++++
Campo elettrostatico sulla super-
ficie di un conduttore sferico ca-
vo carico.
Figura 4.11
E
= 0
σ
E
= —
u
n
ε
0
O
R
C
1
C
2
Σ
C
1
C
2
















