
E
V
0
P
2
P
1
P
2
P
1
+ + + +
u
n
E
d
Σ
E
= 0
4.1 Conduttori in equilibrio
71
troni questi si portano sulla superficie, se si sottraggono, ne risulta carente lo strato
superficiale.
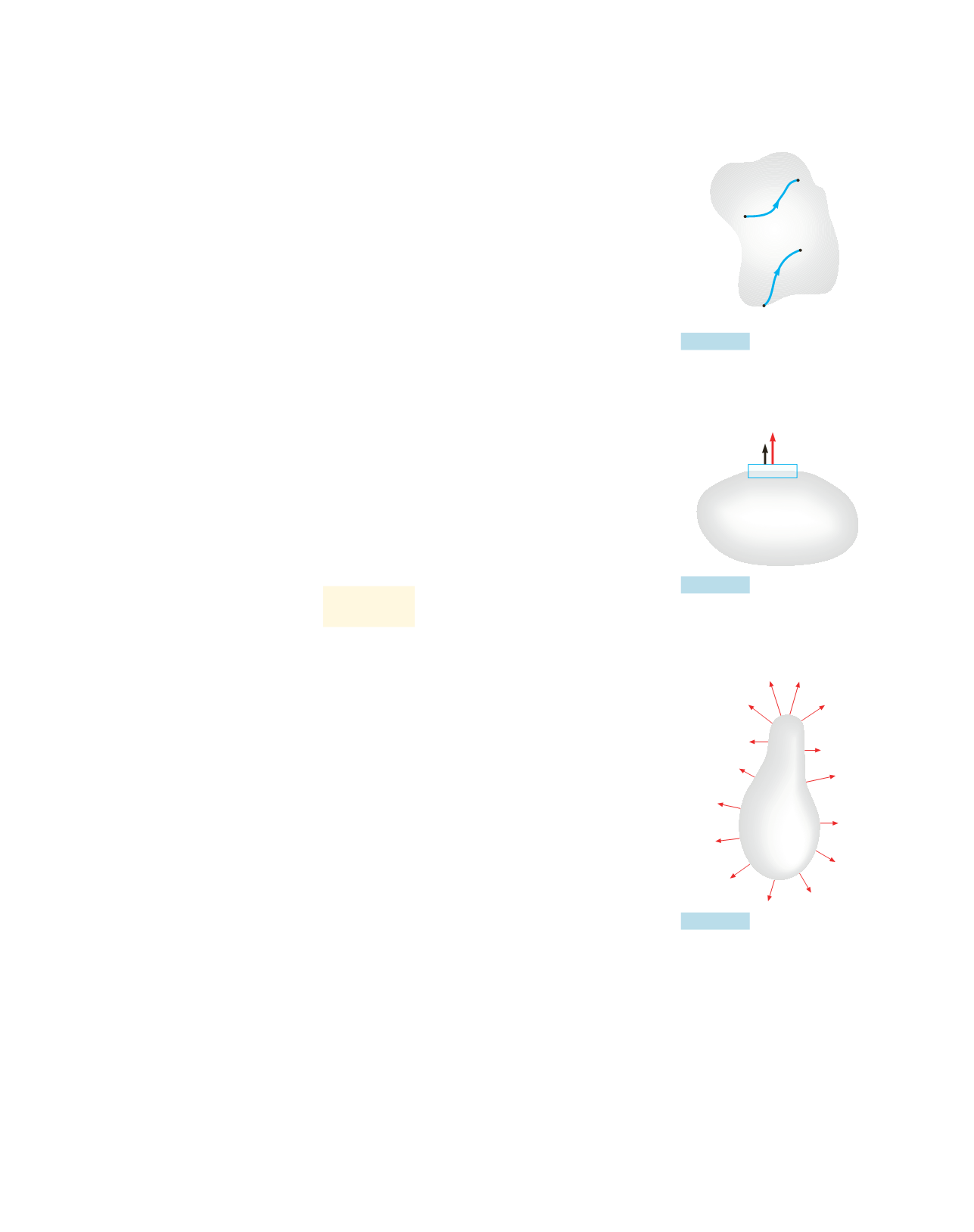
Il potenziale elettrostatico risulta costante in ogni punto del conduttore perché
presi due punti qualsiasi, figura 4.2:
V
(
P
2
) –
V
(
P
1
) = –
∫
P
2
P
1
E
·
d
s
= 0
⇒
V
(
P
2
) =
V
(
P
1
) =
V
0
.
Il risultato è vero anche se uno dei due punti sta sulla superficie del condut-
tore, che risulta quindi essere una
superficie equipotenziale
.
Dato che la superficie del conduttore è equipotenziale, il campo elettrostatico
E
in un punto esterno molto vicino al conduttore è ortogonale alla superficie del
conduttore, indipendentemente dalla forma di questo.
Il valore di
E
si ricava applicando la legge di Gauss ad un cilindro retto di basi
d
Σ
e superficie laterale di area trascurabile rispetto a
d
Σ
, con una base contenuta
all’interno del conduttore, in cui
E
= 0, e l’altra in prossimità immediata del con-
duttore all’esterno, dove il campo elettrostatico
E
è normale alla superficie, figura
4.3. Detta
dq
la carica contenuta all’interno, sulla superficie del conduttore, si ha:
1
1
E
·
u
n
d
Σ
=
E d
Σ
= —
dq
= —
σ
d
Σ
ε
0
ε
0
e quindi:
σ
E
= —
u
n
,
(4.1)
ε
0
risultato noto come
teorema di Coulomb
. Il verso è
uscente
se la densità è
positiva
,
entrante
se è
negativa
.
Si vede che il modulo del
campo elettrostatico
è
maggiore
dove
σ
è
maggiore
, figura
4.4; come giustificheremo più avanti
σ
è maggiore dove il raggio di curvatura della
superficie è minore, fatto che si verifica ad esempio in zone a forma di
punta
. Se il
conduttore possiede una carica notevole la densità sulle punte è molto elevata e
tale è il campo nelle immediate vicinanze; in una rappresentazione grafica le linee
di forza sono molto fitte vicino alle punte. Da questo effetto hanno origine svariati
fenomeni, come la formazione di scintille tra elettrodi di forma appuntita in am-
biente gassoso o l’effluvio di elettroni da punte cariche negativamente, che av-
viene anche nel vuoto.
Un conduttore carico
lontano da altri conduttori
ha dunque una distribuzione su-
perficiale di carica tale che il campo elettrostatico all’interno sia nullo, qualunque
sia la forma del conduttore. In particolare se il conduttore è sferico la carica è di-
stribuita uniformemente; sappiamo infatti dall’esempio 3.1 che una distribuzione
superficiale sferica uniforme di carica dà campo nullo all’interno. Notiamo inoltre
che la carica deve avere lo stesso segno, positivo o negativo, ovunque sulla superfi-
cie: un accumulo di elettroni soltanto in una certa zona sarebbe dovuto esclusiva-
mente a un campo elettrico esterno che non esiste nel caso considerato.
Avvicinando un conduttore, carico o scarico, ad un altro corpo carico, ovvero in-
troducendolo in un campo elettrico esterno
E
, il campo elettrostatico all’interno non
sarebbepiùnullo,ma sarebbedatoda
E
; senonchéquesto fattoprovocaunmovimento
di elettroni che si spostano per l’azione del campo elettrico esterno e si accumulano in
una zona della superficie, lasciando sul resto della superficie un eccesso di carica posi-
tiva: tra queste zone si crea un
campo elettrostatico indotto
E
i
che contrasta il movimento
degli elettroni e si raggiunge l’equilibrio quando
E
+
E
i
= 0 in tutto l’interno del con-
Proprietà del potenziale elettro-
statico in un conduttore carico
in equilibrio.
Figura 4.2
Applicazione della legge di Gauss
per il calcolo del campo elettro-
statico sulla superficie di un con-
duttore carico.
Figura 4.3
Linee di forza nell’intorno della
superficie di un conduttore ca-
rico.
Figura 4.4
















