
72
C A P I T O L O 4
Conduttori. Dielettrici. Energia elettrostatica
duttore. Abbiamo così una distribuzione di
carica elettrica indotta
dei due segni sulla su-
perficie del conduttore che si sovrappone all’eventuale carica elettrica preesistente; in
totale però la carica elettrica del conduttore rimane la stessa poiché la carica elettrica
indotta è la somma algebrica dei due contributi eguali ed opposti. È questa la ragione
del fenomeno dell’
induzione elettrostatica
già descritto nel paragrafo 1.2.
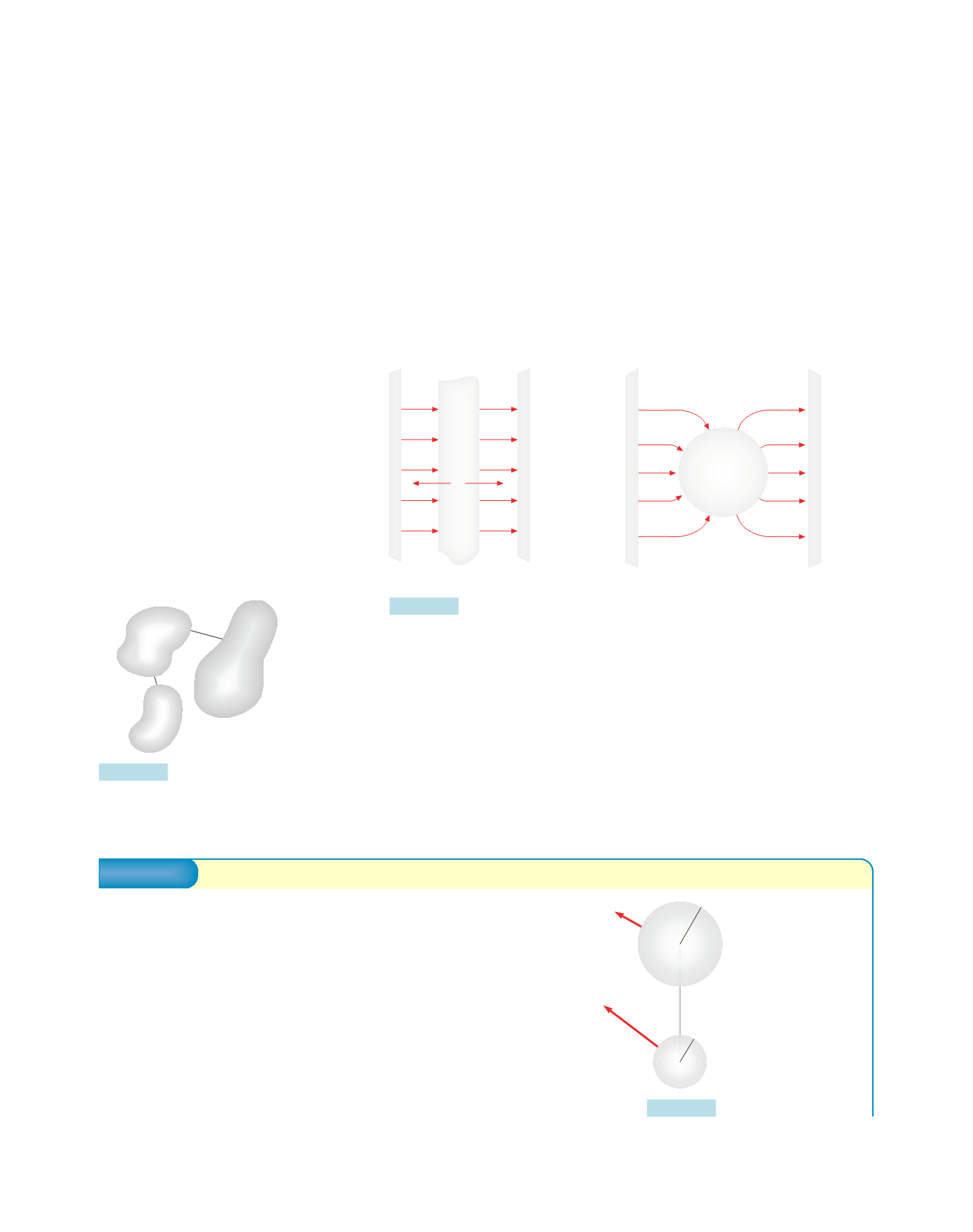
Nella figura 4.5 sonomostrati due esempi: i conduttori sono inizialmente privi di
carica (e tali restano). Nel caso (a) un conduttore a forma di lastra piana è posto tra
due piani uniformemente carichi: sulle facce compare la densità uniforme di carica
σ
i
=
ε
0
E
i
eguale in modulo alla densità
σ
=
ε
0
E
dei piani, con segno tale da produrre
campo elettrostatico nullo dentro la lastra (e invariato fuori dalla lastra).
Nel caso (b) il conduttore è sferico e la densità di carica non può essere uniforme
(darebbe da sola campo elettrostatico nullo all’interno); essa deve invece essere tale
da dare campo elettrostatico uniforme, pari a –
σ
/
ε
0
, in tutta la sfera.
Finora abbiamo parlato di un unico conduttore. Se poniamo a contatto due o
più conduttori, ad esempio collegandoli con un filo conduttore, figura 4.6, si co-
stituisce un
unico corpo conduttore
e in equilibrio vale ovunque la condizione
E
= 0,
V
= costante: i
conduttori a contatto hanno lo stesso potenziale
.
+
+
+
+
+
+
_
_
_
_
_
_
+
+
+
+
+
_
_
_
_
_
+
+
_
_
+
+
_
_
+
+
_
_
+
+
_
_
+
+
_
_
+
_
–
σ
–
σ
i
+
σ
i
+
σ
E
i
(a)
(b)
E
E
Due sfere conduttrici, figura 4.7, di raggi rispettivamente
R
1
e
R
2
, sono poste a distanza molto grande rispetto a
R
1
e
R
2
e
sono collegate tramite un filo conduttore. La carica comples-
siva è
q
. Trascurando la carica presente sul filo, calcolare: la ca-
rica
q
1
e
q
2
presente sulle due sfere e il rapporto tra i campi
elettrostatici
E
1
e
E
2
sulle stesse.
Soluzione
Dal testo capiamo che possiamo porre
q
=
q
1
+
q
2
e
che le sfere sono sufficientemente lontane da poter trascurare
l’induzione elettrostatica che renderebbe non uniformi le di-
stribuzioni di carica sulla superficie. Nel paragrafo 4.1 ab-
biamo detto che due conduttori a contatto hanno lo stesso po-
tenziale, per cui, utilizzando i risultati dell’esempio 3.1:
E
SEMPIO
4.1
Sfere conduttrici a contatto
Lastra di materiale conduttore all’interno di un campo elettrostatico
uniforme (a) e sfera di materiale conduttore all’interno di un campo elet-
trostatico uniforme (b).
Figura 4.5
Sistema di conduttori in contatto
in equilibrio.
Figura 4.6
Figura 4.7
Carica elettrica indotta
V
V
V
E
1
E
2
R
1
R
2
Σ
1
Σ
2
q
1
q
2
















