
4.4 Collegamento di condensatori
81
1 1 1 1
1
––– = –– + –– + –– + … ––– :
(4.16)
C
eq
C
1
C
2
C
3
C
n
in un sistema di condensatori in serie la carica è la stessa su ciascuno, l’in-
verso della capacità equivalente è somma degli inversi delle singole capa-
cità.
La capacità equivalente è sempre minore di quella di ciascun componente.
Ci si rende conto che da un insieme di condensatori di valori dati con oppor-
tuni collegamenti in parallelo o in serie è possibile ottenere capacità equivalenti in
un grande intervallo di valori.
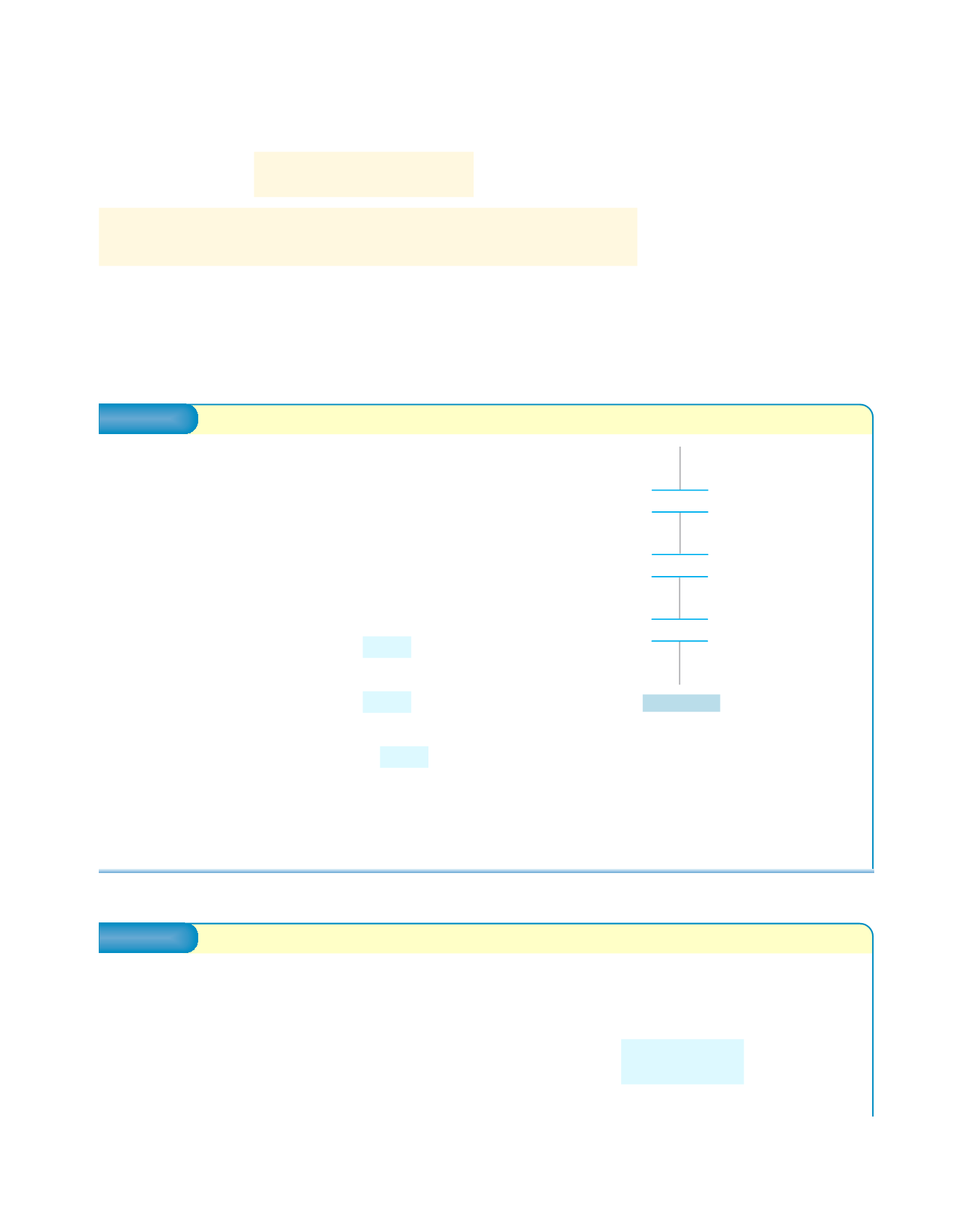
Condensatori in serie
Ai capi di tre condensatori in serie, figura 4.25, c’è una
d.d.p.
V
=
V
B
–
V
A
= 100 V e la capacità equivalente del sistema
è
C
= 100 pF. Calcolare i valori delle capacità
C
1
,
C
2
,
C
3
tali che
rispetto a
V
A
sia
V
1
= 50 V e
V
2
= 70 V.
Soluzione
La carica che si trova su ciascuna armatura è
q
=
C V
= 100 · 10
–12
· 10
2
= 10
–8
C
e i valori richiesti delle capacità sono
q
10
–8
C
1
= ––––––– = –––– = 2 · 10
–10
F = 200 pF ,
V
1
–
V
A
50
q
10
–8
C
2
= ––––––– = –––– = 5 · 10
–10
F = 500 pF ,
V
2
–
V
1
20
q
10
–8
C
3
= ––––––– = –––– = 3.33 · 10
–10
F = 333 pF .
V
B
–
V
2
30
Il sistema si chiama
partitore capacitivo
perché permette di
ripartire una data d.d.p. (in tre parti nel caso specifico). In ge-
nerale, detti
C
i
e
V
i
i valori della capacità e della d.d.p. ai capi
dell’
i
-esimo condensatore, dall’eguaglianza
C
1
V
1
=
C
2
V
2
= … =
C
i
V
i
= …
C
n
V
n
si vede che la d.d.p. si ripartisce in maniera inversamente pro-
porzionale alla capacità:
1 1
1
V
1
:
V
2
: … :
V
n
= ––– : ––– : … : ––– .
C
1
C
2
C
n
E
SEMPIO
4.6
Partitore capacitivo
V
B
V
2
V
1
V
A
C
3
C
2
C
1
Due condensatori di capacità
C
1
e
C
2
hanno un’armatura a
terra e sono caricati con d.d.p.
V
1
e
V
2
, figura 4.26. Si collegano
tra loro le due armature libere e il sistema assume una nuova
condizione di equilibrio con una d.d.p.
V
rispetto alla terra.
Calcolare il valore di
V
.
Soluzione
La carica presente inizialmente nei due conden-
satori è
q
1
=
C
1
V
1
,
q
2
=
C
2
V
2
e la somma rimane la stessa anche nella nuova situazione,
q
= (
C
1
+
C
2
)
V
=
q
1
+
q
2
=
C
1
V
1
+
C
2
V
2
,
da cui si ricava
C
1
V
1
+
C
2
V
2
V
= ––––––––––– ,
C
1
+
C
2
intermedio tra
V
1
e
V
2
.
E
SEMPIO
4.7
Due condensatori in parallelo
Figura 4.25
















