
Alle stesse espressioni si arriva per l’energia elettrostatica di un conduttore carico
isolato immaginando il processo di carica come un trasporto di carica dall’infinito,
dove
V
= 0, alla superficie del conduttore. Ciò torna formalmente con l’idea di con-
siderare un conduttore isolato come un condensatore con un’armatura all’infinito.
Il ragionamento svolto per il calcolo dell’energia del condensatore lega l’ener-
gia alle cariche, che la possiedono in quanto si trovano ad un certo potenziale:
l’energia totale è la somma delle energie potenziali delle singole cariche. È però
possibile trovare un’espressione alternativa dell’energia, legata al campo elettro-
statico prodotto dal sistema di cariche piuttosto che alle sorgenti del campo stesso.
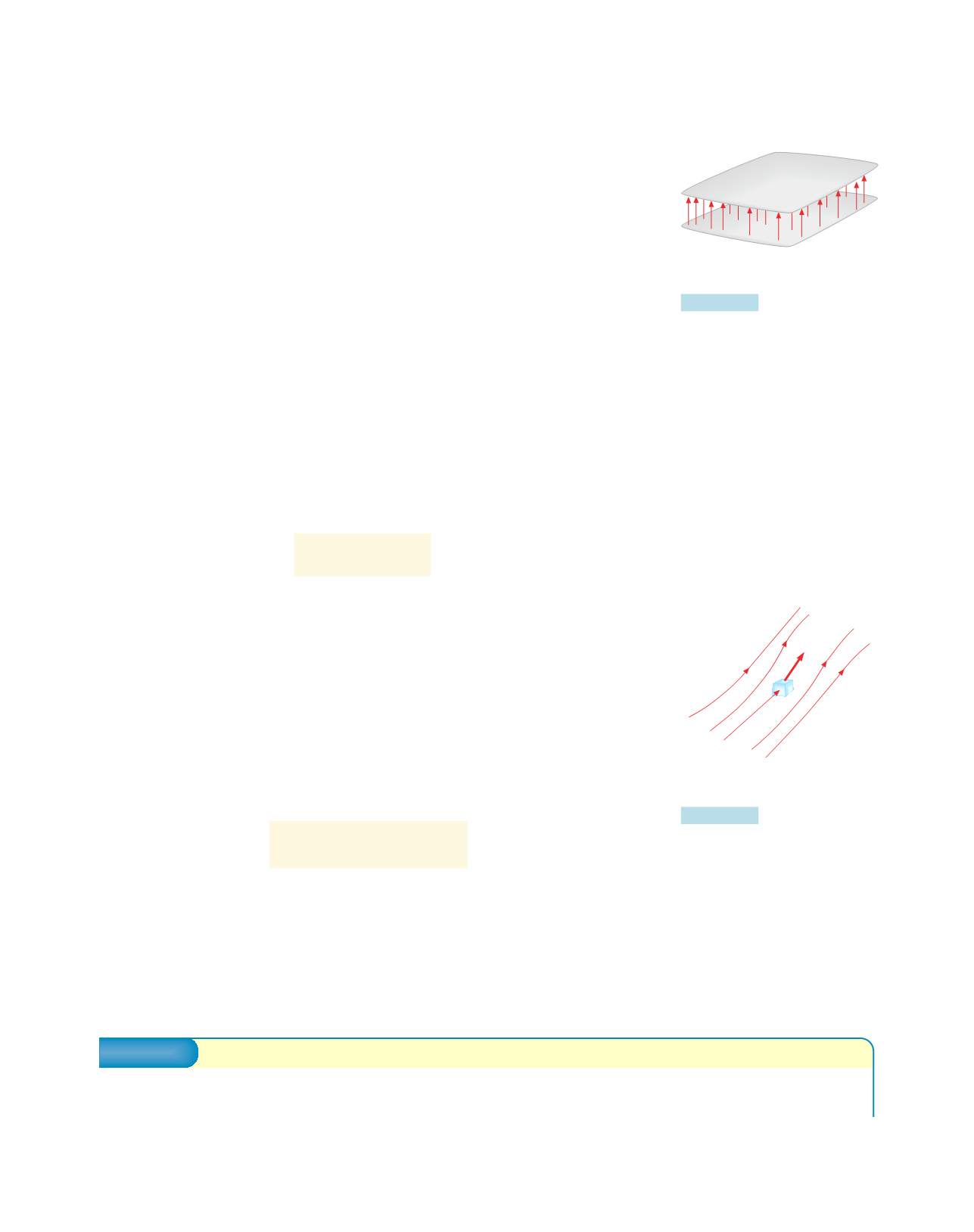
Consideriamo per semplicità un condensatore piano, in cui il campo elettro-
statico tra le armature è uniforme, figura 4.27. Riprendiamo la (4.12) e la rela-
zione
V
=
Eh
:
1
1
ε
0
Σ
1
1
U
e
= ––
CV
2
= –– ––––
E
2
h
2
= ––
ε
0
E
2
Σ
h
= ––
ε
0
E
2
τ
2
2
h
2
2
essendo
τ
=
Σ
h
il volume del condensatore, cioè il volume in cui è definito il campo
elettrostatico. Se facciamo l’ipotesi che l’energia elettrostatica sia distribuita nei
punti in cui c’è campo elettrostatico e che questa distribuzione sia uniforme come
il campo, possiamo dire che la
densità di energia elettrostatica
, ovvero l’energia
elettrostatica per unità di volume, è
U
e
1
u
e
= ––– = ––
ε
0
E
2
,
(4.18)
τ
2
che risulta pertanto
proporzionale al quadrato del campo elettrostatico
.
La generalità di questa formula, in cui non compare alcun elemento caratteri-
stico del sistema per cui il calcolo è stato eseguito, ma soltanto il valore del campo
e una proprietà del mezzo (in questo caso il vuoto), suggerisce che (4.18) si possa
applicare a qualsiasi situazione. In effetti si può dimostrare che in una regione in
cui è definito un campo elettrostatico l’energia contenuta in ogni volume infinite-
simo
d
τ
, al cui interno il campo elettrostatico vale
E
, figura 4.28, è
1
dU
e
=
u
e
d
τ
= ––
ε
0
E
2
d
τ
;
2
l’energia totale del campo elettrostatico si ottiene integrando su tutto il volume in
cui il campo elettrostatico è diverso da zero:
1
U
e
=
∫
dU
e
=
∫
––
ε
0
E
2
d
τ
.
(4.19)
2
Questa energia corrisponde al lavoro speso per costruire la distribuzione di ca-
riche che dà origine al campo elettrostatico.
Le (4.18) e (4.19) valgono per qualsiasi campo elettrico, indipendentemente
dalla sua natura. Utilizzeremo la (4.18) nel paragrafo 10.4 relativamente al campo
elettrico di un’onda elettromagnetica.
Nel SI l’unità di misura della densità di energia elettrostatica è joule/m
3
( J/m
3
).
Densità di energia elettrostatica
h
Σ
1
U
e
= ––
ε
0
E
2
τ
2
E
P
d
τ
Calcolare l’energia elettrostatica di un condensatore sfe-
rico di raggi
R
1
e
R
2
.
Soluzione
Impostiamo il calcolo sulla (4.19) utilizzando
quanto visto nell’esempio 4.2: il campo tra le armature del
E
SEMPIO
4.8
Energia elettrostatica di un condensatore sferico
4.5 Energia del campo elettrostatico
83
Figura 4.27
Figura 4.28
Energia elettrostatica nell’intor-
no di un punto.
Energia elettrostatica immagaz-
zinata all’interno di un conden-
satore carico.
1
dU
e
= ––
ε
0
E
2
d
τ
2
















