
Olografia
655
Diffrazione di un ostacolo piano
Prendiamo infine in considerazione un ostacolo piano opaco delimitato da uno spigolo
netto, come potrebbe essere il bordo di una fenditura rettilinea indefinita o il filo di una lama.
L’onda incidente è piana e monocromatica, con fronte d’onda parallelo al piano contenente
l’ostacolo.
Ponendosi in un punto
P
a distanza
r
0
dal bordo e costruendo il relativo sistema di zone di
Fresnel, si osserva che queste sono tutte tagliate a metà dal bordo dell’ostacolo. Se
E
è
l’ampiezza del campo elettrico prodotto in
P
dall’intero fronte d’onda, l’ampiezza in presen-
za dell’ostacolo è
E
P
=
E
/ 2 e l’intensità
I
P
=
I
/ 4. In un punto
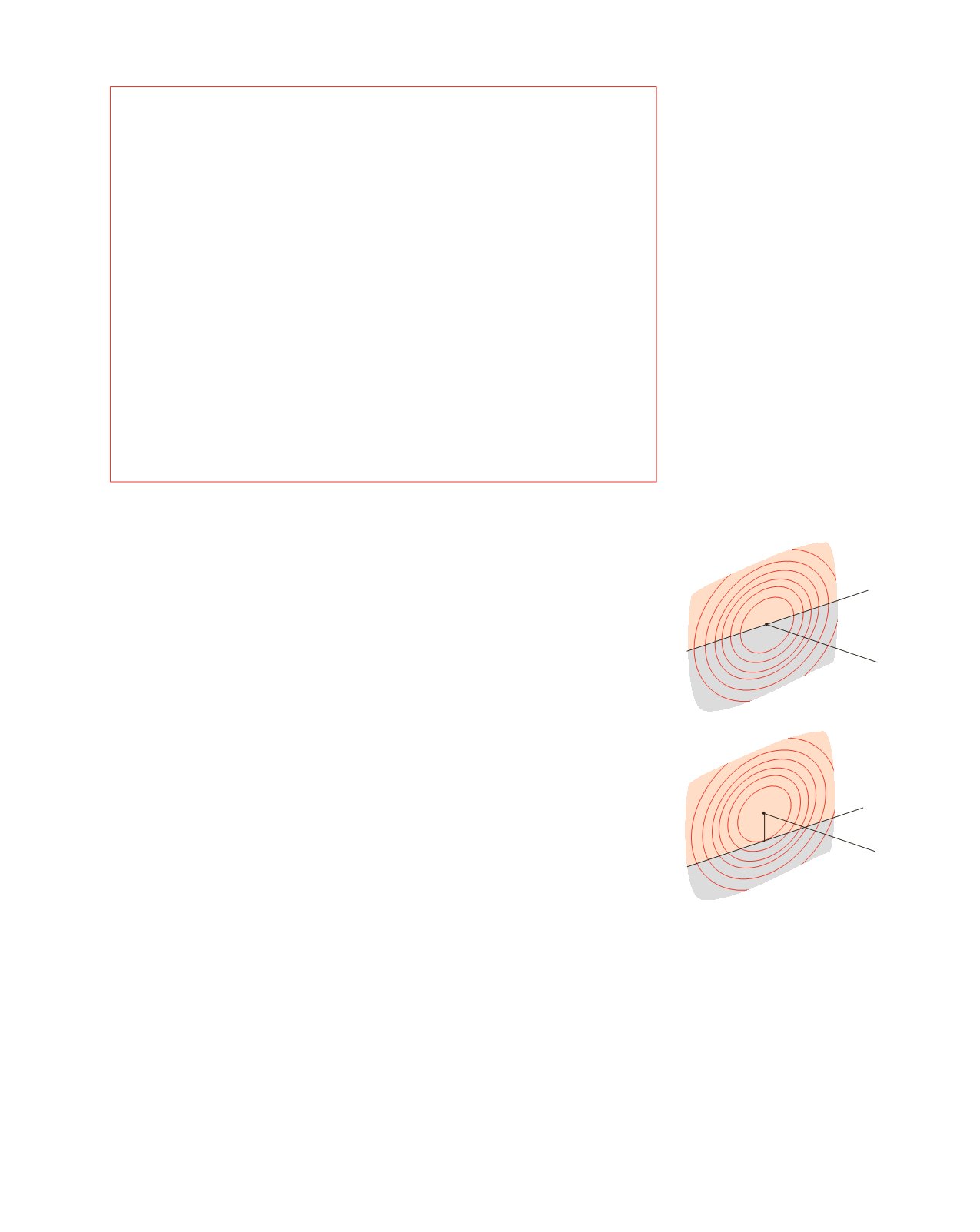
P
1
, posizionato come mostrato
in figura 16.43 e distante da
P R
1
=
r
0
l
, la prima zona di Fresnel contribuisce completa-
mente all’intensità; per le altre si può dire che ciascuna zona pari è tagliata un po' meno della
successiva zona dispari, così che il contributo da sottrarre è minore che in assenza dell’osta-
colo e l’intensità in
P
1
risulta maggiore dell’intensità
I
senza ostacolo. Nella figura 16.44 è
mostrato l’andamento dell’intensità trasversalmente all’asse
OP
: si vede che c’è intensità
nella zona d’ombra geometrica, che le variazioni si hanno in vicinanza della proiezione del
bordo e che allontanandosi da questa l’intensità tende al valore costante
I
. Analogamente al
crescere della distanza
r
0
questi effetti di diffrazione tendono a scomparire. Infine nella figu-
ra 16.45 è mostrata la figura di diffrazione di una fenditura (due bordi con spigolo netto) in
vicinanza della stessa e all’infinito, dove si ritrova il risultato di Fraunhofer.
16.9 Olografia
Un’onda piana monocromatica che si propaga lungo l’asse
x
e incide su una lastra foto-
grafica produce su questa un annerimento che dipende localmente dall’intensità che ha col-
pito la lastra durante il tempo di esposizione e che quindi, per l’onda piana, è uniforme.
Supponiamo che in un punto
P
, posto a distanza
x
0
dalla lastra, ci sia una sferetta molto pic-
cola, la quale diffonde, attraverso unmeccanismo del tipo discusso nel paragrafo 13.8, la luce
incidente dando origine ad un’onda sferica coerente con l’onda primaria e quindi capace di
interferire con essa.
In un punto
Q
della lastra
L
distante
r
da
P
e
z
dall’asse
x
si osserva pertanto l’interferen-
za tra l’onda primaria
E
rif
, che chiamiamo
onda di riferimento
, e l’onda sferica
E
ogg
prove-
niente da
P
, che chiamiamo
onda oggetto
:
E
rif
=
E
0
cos (
k x
0
–
w
t
) ,
E
ogg
=
E
(
r
) cos (
kr
–
w
t
) .
Esempio 16.12
Un’onda piana con
l
= 0.685
μ
m incide perpendicolarmente su un disco opaco di raggio
R
= 2 mm. Confrontare l’intensità osservata in un punto
P
1
sull’asse del disco alla
distanza
r
1
= 5.84 m con l’intensità
I
0
in assenza del disco. Ripetere il calcolo per un
punto
P
2
distante
r
2
= 2.92 m.
Soluzione
Nella posizione
r
1
, riprendendo i risultati dell’esempio 16.11, il disco opaco copre la
prima zona di Fresnel relativa a
P
1
, per cui
E
foro
= 2
E
se
E
è l’ampiezza che sarebbe pro-
dotta dal fronte d’onda completo. Pertanto
E
disco
=
E
–
E
foro
= –
E
,
I
disco
=
I
,
l’intensità in
P
1
è la stessa di quella in assenza del disco opaco. In
P
2
, a distanza
r
2
=
r
1
/2,
E
foro
0 per cui
E
disco
=
E
–
E
foro
=
E
,
I
disco
=
I
e si ha la stessa intensità che a distanza
r
1
.
La figura di diffrazione completa consiste ancora di una serie di anelli scuri e chiari che
circondano
in ogni caso
un dischetto centrale chiaro.
O
r
0
P
P
1
O
R
1
bordo dello
ostacolo
bordo dello
ostacolo
E
E
P
= ––
2
Figura 16.43
















