
Fenomeni di diffrazione di Fresnel
653
Reticolo zonato di Soret
Nel punto
P
si può avere un’intensità notevole se si interpone sul fronte d’onda, a distan-
za
r
0
da
P
, una sottile lastra di vetro in cui sono tracciate una serie di corone circolari opache
disposte in modo da intercettare, per quel valore di
r
0
e
l
, le zone dispari di Fresnel lasciando
scoperte quelle di ordine pari o viceversa. In tali condizioni si ha solo interferenza costrutti-
va (
E
P
=
E
2
+
E
4
+
E
6
+ … oppure
E
P
=
E
1
+
E
3
+
E
5
+ …) e l’intensità in
P
risulta molto mag-
giore che se si lasciassero interferire tutte le porzioni del fronte d’onda.
Il dispositivo è detto
reticolo zonato di Soret
. Se fissiamo la lunghezza d’onda
l
e le
dimensioni del dischetto centrale, cioè il raggio
R
1
, sono automaticamente fissati tutti i raggi
delle zone di Fresnel dalla condizione che le aree delle corone circolari siano eguali ed è fis-
Fresnel e in
P
si ha un massimo di intensità. Nel nostro caso
R
2
4 · 10
–6
r
0
= ––– = ––––––––––– = 5.84 m .
l
0.685 · 10
–6
Al crescere di
r
0
i raggi delle zone di Fresnel crescono e quindi se
r
0
supera 5.84 m il
foro coincide con una parte interna alla prima zona di Fresnel: ciò vuol dire che
all’aumentare di
r
0
oltre 5.84 m l’intensità decresce monotonamente senza presentare
massimi o minimi.
Osserviamo che per
r
0
= 5.84 m i raggi che provengono dal bordo del foro hanno rispet-
to all’asse un’inclinazione
2 · 10
–3
q
= –––––––– = 3.4 · 10
–4
rad = 0.02 gradi
5.84
e possono essere considerati praticamente paralleli. Guardando la figura di diffrazione
su uno schermo posto oltre 5.84 m si nota che essa tende, allontanando lo schermo, alla
figura di diffrazione di Fraunhofer, discussa nel paragrafo 16.3.
Avviciniamo ora lo schermo riducendo il valore di
r
0
al di sotto di 5.84 m. Troviamo
massimi di intensità
nel punto
P
ogni qual volta
R
2
=
nr
0
l
con
n
dispari, ovvero quando
R
2
r
0
= –––––
n
= 3, 5, 7, …
n
l
r
3
= 1.95 m ,
r
5
= 1.17 m ,
r
7
= 0.83 m , … .
Si hanno invece
minimi di intensità
per quelle distanze
r
0
che soddisfano alla condizio-
ne
R
2
r
0
= ––––
n
= 2, 4, 6, …
n
l
r
2
= 2.92 m ,
r
4
= 1.46 m ,
r
6
= 0.97 m , … .
Le distanze tra le posizioni di massimi e minimi diminuiscono avvicinandosi al foro e
diminuiscono anche le intensità dei massimi perché sono sempre di più le zone di
Fresnel che contribuiscono. Le figure di diffrazione sono sempre costituite da corone
circolari alternativamente chiare e scure, con il centro chiaro alle distanze
r
1
,
r
3
,
r
5
, … e
scuro alle distanze
r
2
,
r
4
,
r
6
, … .
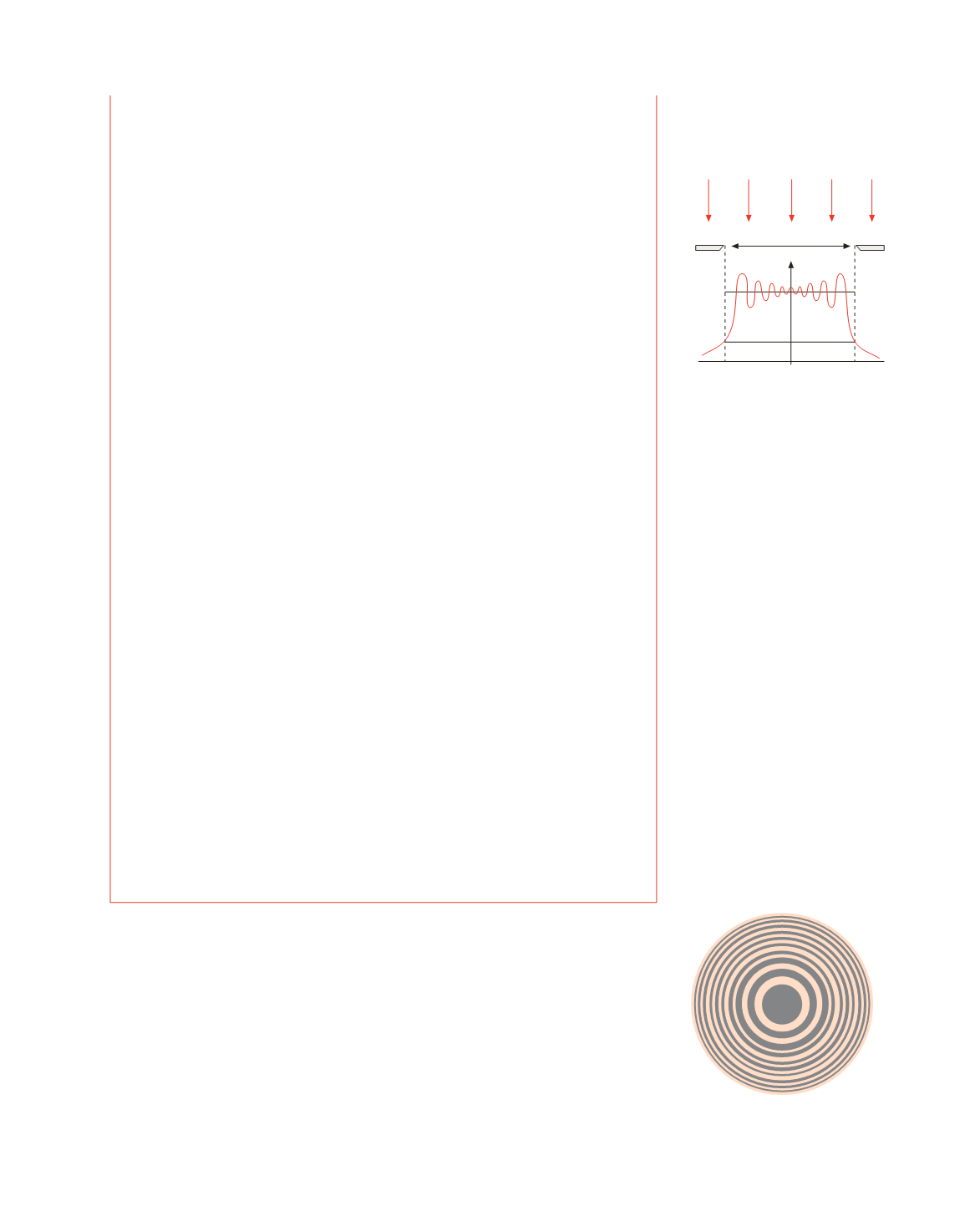
Ponendosi in una posizione di massimo abbastanza vicina al foro, in modo che questo
copra molte zone di Fresnel, si trova che la variazione radiale dell’intensità è quella
mostrata in figura 16.39: i massimi corrispondono alle corone circolari chiare e i mini-
mi alle corone circolari scure (vedi figura 16.38). Detto
I
0
il valor medio dell’intensità si
vede che in corrispondenza al bordo del foro l’intensità è
I
0
/ 4 e che c’è intensità nella
zona d’ombra geometrica.
2
R
I
I
0
I
0
/4
Figura 16.39
Figura 16.40
















