
Fenomeni di diffrazione di Fresnel
651
16.8 Fenomeni di diffrazione di Fresnel
Abbiamo già osservato nel paragrafo 16.1 che i fenomeni di diffrazione di Fresnel hanno
luogo quando o la sorgente delle onde o il punto di osservazione o entrambi sono a distanza
finita dall’apertura o dall’ostacolo che perturbano il fronte d’onda.
Dato che la trattazione analitica è abbastanza complicata, ci limitiamo a discutere alcuni
casi in cui un’onda piana incide su un’apertura praticata su uno schermo opaco o su un osta-
colo e l’osservazione avviene a distanza finita da questi, ma pur sempre grande rispetto alla
lunghezza d’onda
l
della luce incidente. Per il calcolo utilizziamo un metodo elaborato dallo
stesso Fresnel che consiste nel suddividere il fronte d’onda piano incidente in zone opportu-
namente definite, ognuna delle quali viene vista dal punto
P
in cui calcoliamo gli effetti della
diffrazione come sorgente di onde sferiche secondarie. Si tratta cioè di una applicazione par-
ticolare del principio di Huygens-Fresnel, adatta al problema che si vuole risolvere.
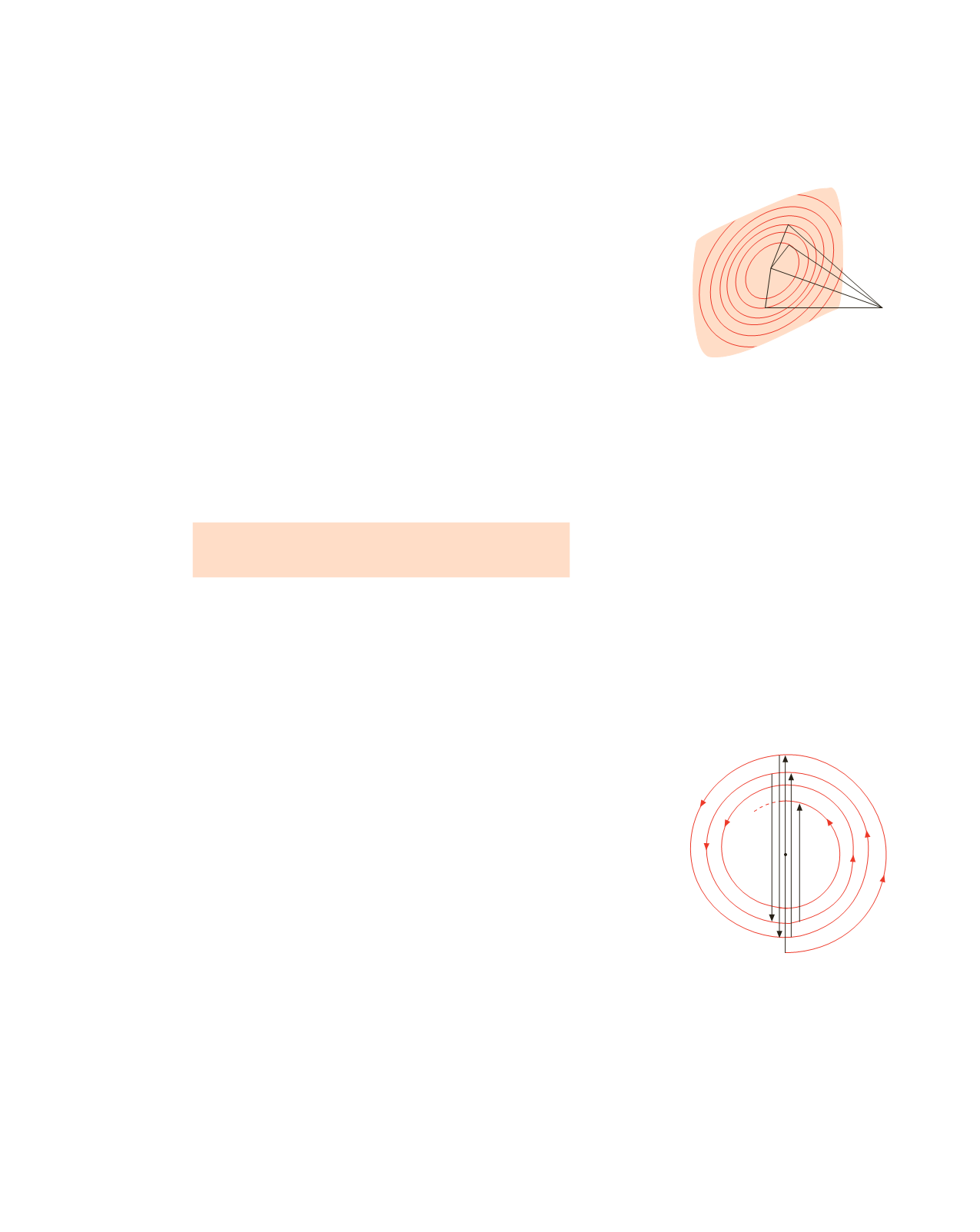
Con riferimento alla figura 16.33 consideriamo un fronte d’onda piano che si propaga
verso
P
e indichiamo con
r
0
=
OP
la distanza di
P
dal fronte d’onda. Suddividiamo questo in
tante zone anulari concentriche aventi
O
come centro, definite dalla condizione che le distan-
ze da
P
del bordo interno e del bordo esterno di ciascuna zona differiscano di
l
/ 2. Pertanto il
bordo del disco centrale, detto
prima zona di Fresnel
, dista da
P r
1
=
r
0
+
l
/ 2, il bordo ester-
no del primo anello, detto seconda zona di Fresnel, dista da
P r
2
=
r
1
+
l
/ 2 =
r
0
+
l
e così
via, come indicato nella figura. In generale quindi
l
l
r
n
=
r
n
– 1
+ ––– =
r
0
+
n
––– ,
n
= 1, 2, 3, … .
2
2
I raggi delle circonferenze che delimitano le
zone di Fresnel
sono dati da
l
l
2
R
2
n
=
r
2
n
–
r
2
0
=
(
r
0
+
n
–––
)
2
–
r
2
0
=
n r
0
l
+
n
2
–––
n r
0
l
,
(16.16)
2
4
dove l’approssimazione è consistente con l’ipotesi
l
<<
r
0
.
Il campo elettrico in
P
si ottiene come somma dei campi elettrici
E
n
provenienti dalle sin-
gole zone. Osserviamo che le aree delle zone di Fresnel,
S
n
=
p
(
R
2
n
–
R
2
n
– 1
) =
p
[
n r
0
l
– (
n
– 1)
r
0
l
] =
p
r
0
l
,
risultano tutte eguali tra loro, non dipendendo da
n
. Quindi le ampiezze delle onde emesse
dalle varie zone sono diverse in
P
soltanto a causa del
fattore di inclinazione
e della distanza,
diminuendo al crescere dell’ordine
n
della zona.
La valutazione del campo elettrico risultante
E
P
viene compiuta applicando il metodo dei
vettori rotanti. Ciascuna zona finita è considerata a sua volta come formata da un numero infi-
nito di elementi di superficie anulari infinitesime, ognuna delle quali emette un’onda di
ampiezza infinitesima. La differenza di fase tra le onde emesse dai bordi interno ed esterno di
ciascuna zona è
2
p
2
p l
d
= –––– (
r
n
–
r
n
–1
) = –––– ––– =
p
.
l
l
2
Ciò significa che disegnando gli infiniti vettori infinitesimi relativi alla prima zona di Fresnel
otteniamo una semicirconferenza il cui diametro
OA
dà il campo elettrico
E
1
dell’onda emes-
sa dalla prima zona (vedi figura 16.34). Per la seconda zona di Fresnel, partendo da
A
abbia-
mo ancora una semicirconferenza il cui diametro
AB
rappresenta il campo
E
2
; il punto
B
non
coincide con
O
in quanto il modulo
E
2
<
E
1
, come si è giustificato sopra. Proseguendo con la
stessa costruzione si intuisce che il punto finale è il punto
O
', centro del segmento
OA
, per cui
OO
', rappresentazione di
E
P
, è la metà di
OA
, rappresentazione di
E
1
:
1
1
E
P
= ––
E
1
,
I
P
= ––
I
1
.
2
4
L’intensità luminosa in
P
prodotta da un fronte d’onda indefinito è pari ad
un quarto
dell’intensità prodotta dalla prima zona: la diminuzione è dovuta all’interferenza distruttiva
tra le varie zone.
fronte d’onda
R
3
R
1
R
2
l
r
1
=
r
0
+ –– ,
r
2
=
r
0
+
l
2
l
r
3
=
r
0
+ 3 –– , …
2
r
3
r
1
r
0
r
2
P
O
Figura 16.33
A
C
E
O
'
D
B
O
OA
=
E
1
,
AB
=
E
2
,
BC
=
E
3
, …
OO
' =
E
P
Figura 16.34
















