
Spettroscopia con il reticolo di diffrazione
647
16.7 Spettroscopia con il reticolo di diffrazione
I reticoli di diffrazione hanno un’utilizzazione molto importante nell’analisi
della radiazione elettromagnetica visibile emessa dalle varie sostanze opportuna-
mente eccitate,
analisi
che viene chiamata
spettroscopica.
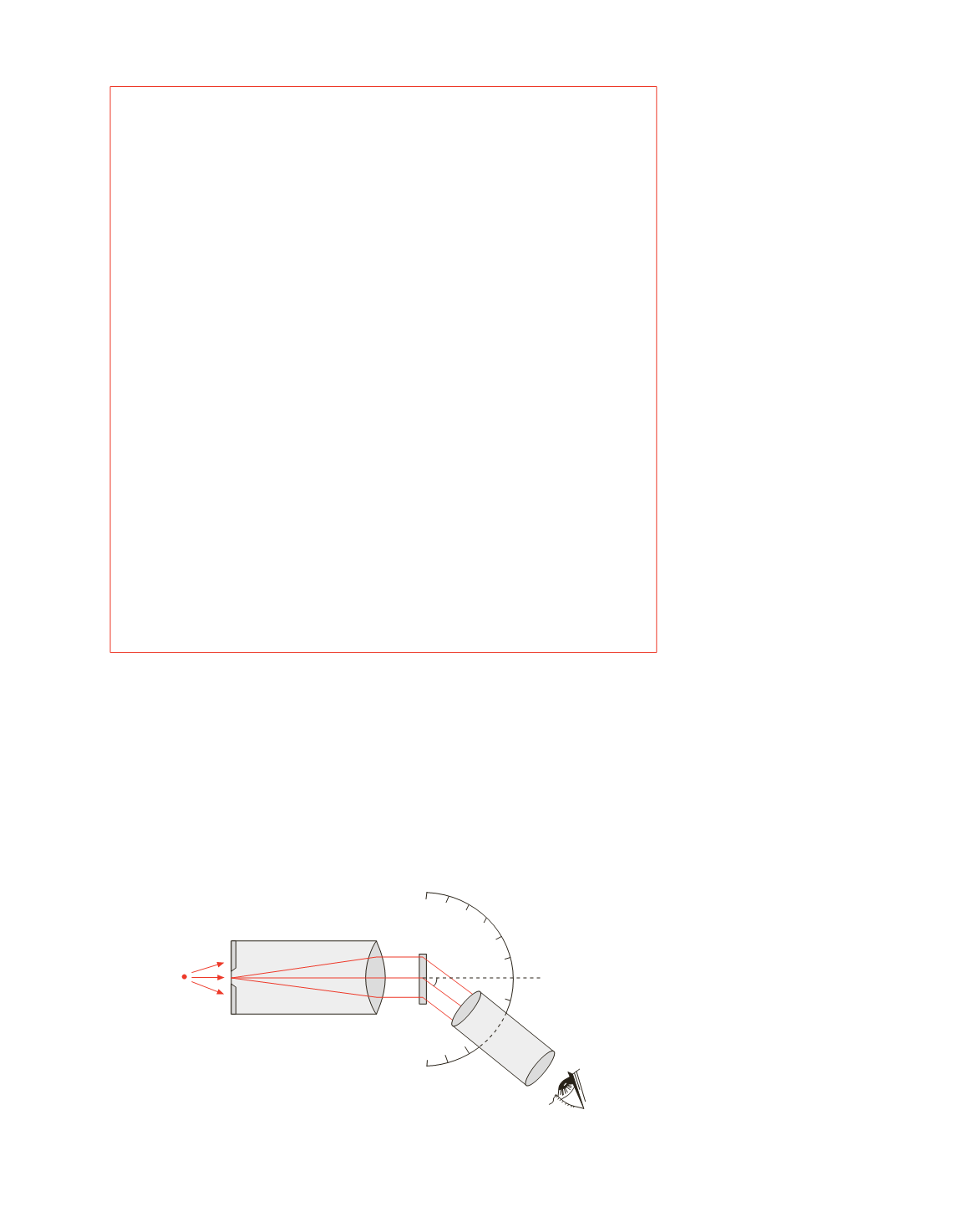
L’apparecchio usato per la misura delle lunghezze d’onda emesse da una sor-
gente è mostrato schematicamente in figura 16.28; esso costituisce un esempio di
spettroscopia a reticolo di diffrazione.
Esempio 16.10
Un reticolo di diffrazione lungo
L
= 2.5 cm ha
N
= 4000 fenditure. Esso è illuminato con
una luce verde di lunghezza d’onda
l
= 0.546
m
m, emessa da una lampada a vapori di
mercurio. Calcolare il potere dispersivo al second’ordine e la minima differenza
Dl
nell’intorno di
l
che è risolvibile, sempre al second’ordine.
Soluzione
Il passo del reticolo è
d
= 6.25
μ
m e il massimo del second’ordine si forma per sen
q
2
=
2
l
/
d
= 0.175, per cui
q
2
= 0.176 rad = 10.1. La larghezza angolare (16.12) vale
2
l
Dq
2
= ––––––– = 4.4 · 10
–5
rad = 2.5 · 10
–3
gradi .
L
cos
q
2
Il potere dispersivo e il potere risolutivo al second’ordine sono
2
D
= –––––––– = 0.325 rad/
m
m = 18.6 gradi/
m
m ,
R
= 2 · 4000 = 8 · 10
3
.
d
cos
q
2
L’intervallo
Dl
che si può risolvere vale
Dl
=
l
/
R
= 6.83 · 10
–5
mm = 6.83 · 10
–2
nm
(
Dl
/
l
= 1.25 · 10
–4
) .
Utilizzando i valori trovati di
Dl
e della dispersione
D
si ha, per la separazione angola-
re corrispondente a
Dl
,
Dq
=
D
Dl
= 2.2 · 10
–5
rad
e si verifica che questo valore, essendo pari a metà della larghezza angolare
Dq
2
prima
calcolata, è giustamente la separazione angolare che ci sarebbe tra due massimi dovuti
alle lunghezze d’onda
l
e
l
+
Dl
in condizioni di Rayleigh.
C
R
F
L
1
L
2
L
3
T
q
S
Figura 16.28
















