
646
Diffrazione
l
1
l
1
l
2
l
1
m
––– + ––––
m
–––
⇒
m
(
l
2
–
l
1
) ––– ,
d Nd d
N
l
1
l
2
l
2
l
2
m
–––
m
––– – ––––
⇒
m
(
l
2
–
l
1
) ––– .
d d
Nd
N
Sommando si ottiene
m
(
l
2
–
l
1
) (
l
1
+
l
2
) / 2
N
; si pone
l
= (
l
1
+
l
2
) / 2,
Dl
=
l
2
–
l
1
e si definisce
potere risolutivo
del reticolo all’ordine
m
la grandezza
l
R
= –––– =
m N
,
(16.15)
Dl
la quale esprime, per una data
l
, la differenza
Dl
risolvibile. Il
potere risolutivo
risulta
proporzionale al numero totale di fenditure
e aumenta con l’ordine dello
spettro, ma non dipende dal passo del reticolo.
Osserviamo che la dispersione e il potere risolutivo si riferiscono a proprietà
diverse: un reticolo con passo piccolo ha una buona dispersione, ma se è piccolo
anche il numero di fenditure (al limite
N
= 2) esso non è adatto a separare lunghez-
ze d’onda molto vicine: i centri dei massimi sono ben distanziati, ma i massimi stes-
si sono larghi. Invece un reticolo con passo maggiore, ma con un gran numero di
fenditure, ha dispersione minore e potere risolutivo superiore, essendo i massimi
molto stretti.
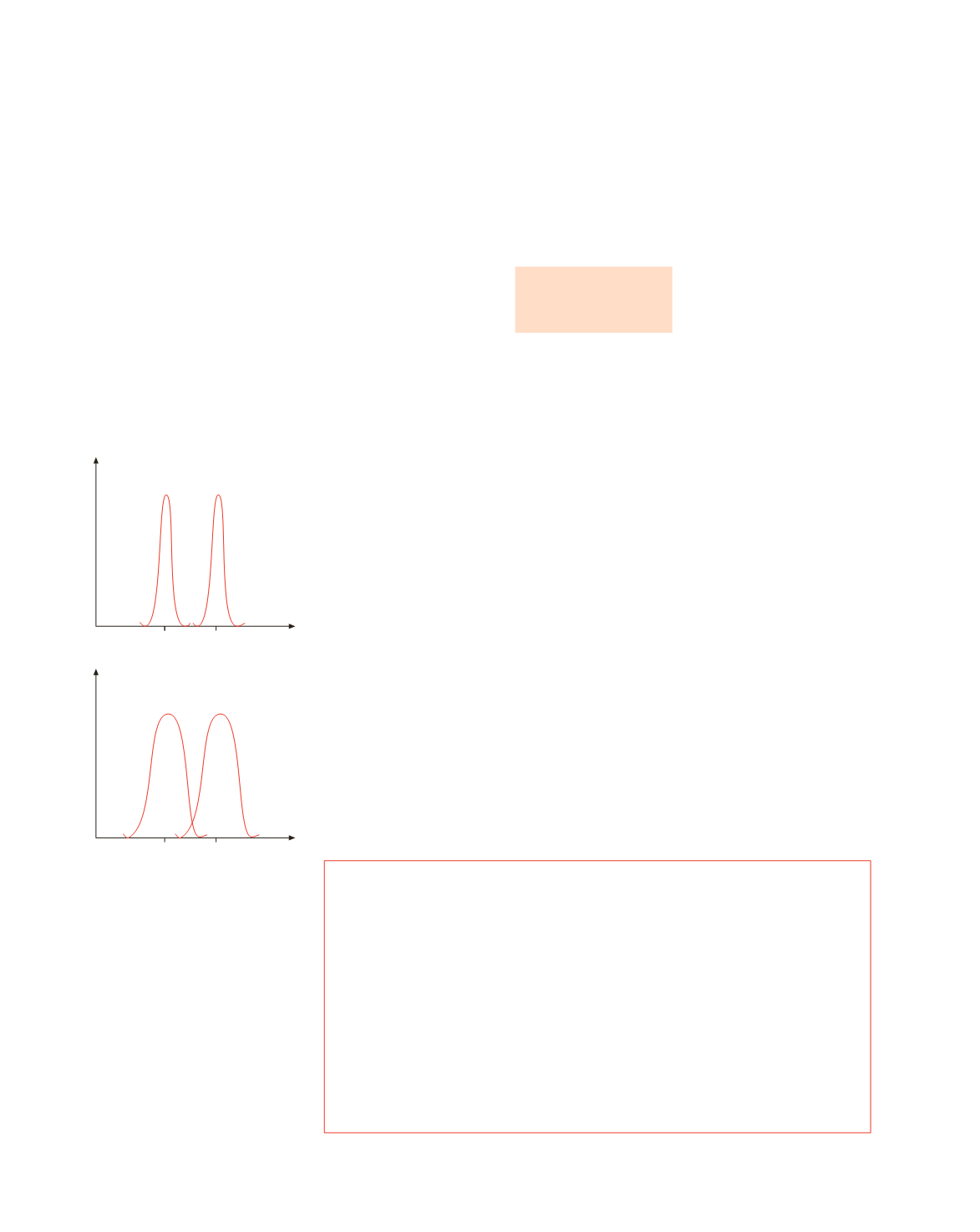
Nella figura 16.27 sono riportate le intensità dei massimi di ordine
m
di due lun-
ghezze d’onda, generati da due reticoli aventi la stessa dispersione e potere risoluti-
vo diverso; tali reticoli hanno evidentemente passo eguale e differiscono per il
numero totale di fenditure ovvero per la larghezza:
N
1
>
N
2
,
L
1
=
N
1
d
>
L
2
=
N
2
d
. È
chiaro che con
d
piccolo e
N
grande si ha il risultato migliore sia per
D
che per
R
.
C’è da dire infine che malgrado la dispersione e la risoluzione non dipendano
esplicitamente dalla larghezza
a
delle fenditure, questo parametro fissa in pratica il
massimo valore di
m
utilizzabile e quindi i massimi valori di
D
e
R
, come si è visto
nella discussione sull’intensità degli spettri di ordine superiore (paragrafo 16.5).
I
/
I
m
Potere risolutivo
I
/
I
m
N
1
N
2
<
N
1
sen
q
sen
q
l
1
m
–––
d
l
2
m
–––
d
l
1
m
–––
d
l
2
m
–––
d
Figura 16.27
Esempio 16.9
Una lampada al sodio, contenente sodio gassoso eccitato con una scarica elettrica, emet-
te due lunghezze d’onda molto vicine, di valori
l
1
= 589.0 nm e
l
2
= 589.6 nm. Quante
linee deve avere un reticolo affinché
l
1
e
l
2
siano appena risolvibili nello spettro del
second’ordine?
Soluzione
Si richiede un potere risolutivo
l
589.3
R
= –––– = –––––– = 982
10
3
.
Dl
0.6
Da (16.15) con
m
= 2 si ricava
N
= 500.
















