
644
Diffrazione
p
a
sen
q
sen ––––––––
l
lim
[
––––––––––––––
]
2
= 1
a
/
l
→
0
p
a
sen
q
––––––––
l
e si ritrova appunto la (15.14), dedotta nell’ipotesi che l’intensità di ciascuna sorgente
fosse costante al crescere di
q
.
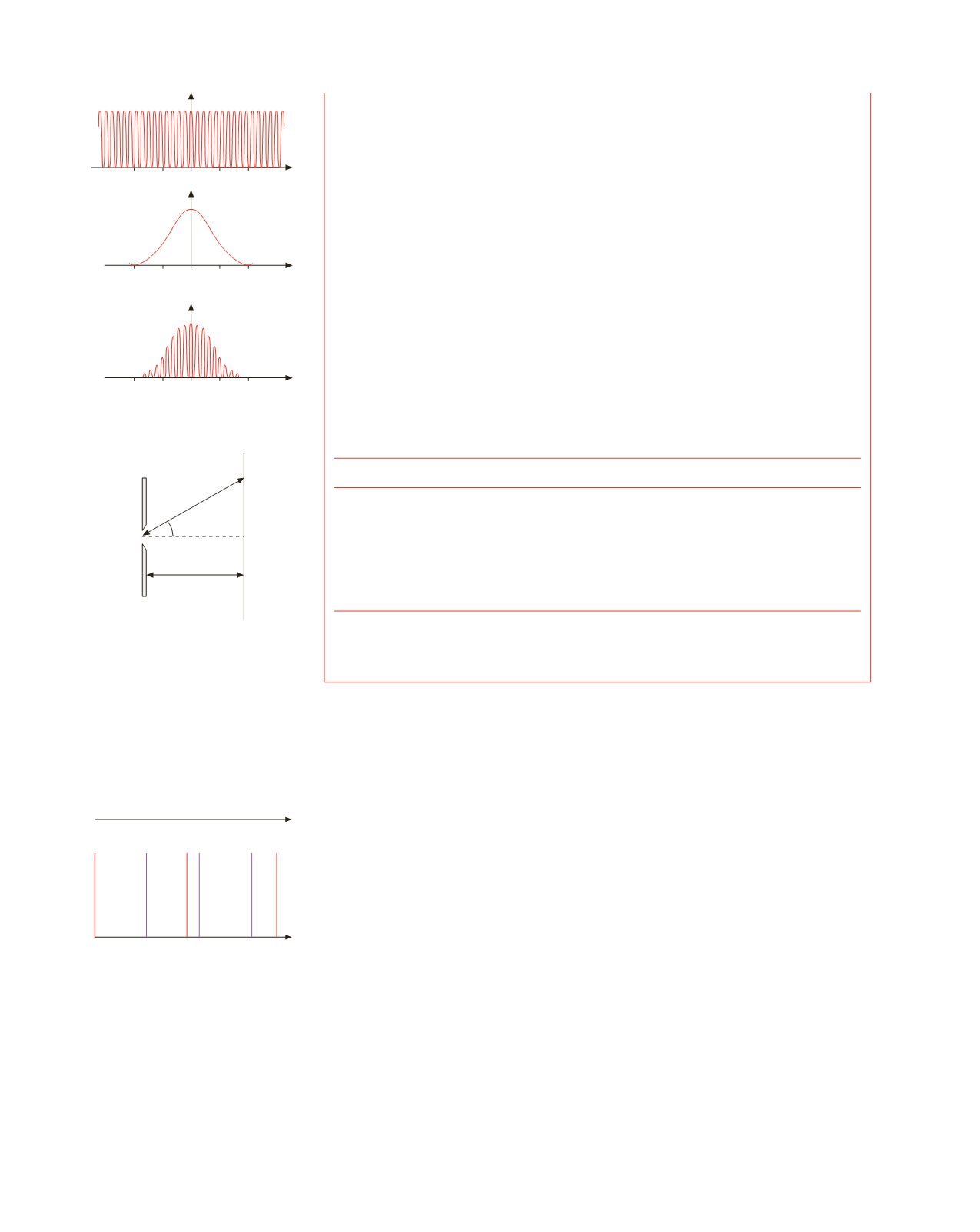
Nella figura 16.23, calcolata numericamente per
l
= 0.5
m
m, sono riportati separata-
mente i vari termini. Poiché
a
/
d
= 1/10 la decima frangia è assente; le frange corrispon-
denti a
m
= 8 e
m
= 9 hanno, applicando (16.13),
R
8
= 0.055 e
R
9
= 0.012. Sono così
osservabili, nell’ipotesi
R
m
> 0.05, la frangia centrale e 8
×
2 = 16 frange laterali. È dun-
que la diffrazione dovuta all’apertura finita delle fenditure la causa fisica principale che
limita l’osservazione di un gran numero di frange d’interferenza.
Gli altri fattori correttivi finora trascurati interverrebbero solamente se si potessero
osservare frange ad angoli molto grandi. Essi sono dovuti al fattore di inclinazione e alla
maggior distanza dalla fenditura dei punti dello schermo lontani dal centro; nell’ipotesi
che una fenditura emetta un’onda cilindrica, l’intensità diminuisce come 1/
r
e rispetto al
centro invece che 1/
f
ci vuole 1/ (
f
/ cos
q
) = cos
q
/
f
, come si vede nella figura 16.24.
Complessivamente il fattore di riduzione angolare risulta
f
2
(
q
) cos
q
; alcuni valori sono
riportati nella tabella.
q
f
2
(
q
)
cos
q
f
2
(
q
) cos
q
0°
1
1
1
5°
0.996
0.996
0.992
15°
0.966
0.966
0.933
30°
0.871
0.866
0.754
45°
0.729
0.707
0.515
60°
0.563
0.500
0.282
Per valori piccoli di
q
la correzione è quasi trascurabile (< 1% fino a 5.7°, < 5% fino a
12.9°), c’è solo l’effetto della diffrazione.
I
(
q
)
I
(
q
)
I
(
q
)
–10° –5° 0° 5° 10°
q
–10° –5° 0° 5° 10°
q
–10° –5° 0° 5° 10°
q
Figura 16.23
P
f
f
––––
cos
q
q
Figura 16.24
Il reticolo descritto finora è detto
reticolo
funzionante in
trasmissione
; se le inci-
sioni vengono fatte su una superficie riflettente abbiamo un reticolo funzionante in
riflessione, per il quale si svolgono considerazioni analoghe.
16.6 Potere dispersivo e potere risolutivo di un reticolo di diffrazione
Se la sorgente che illumina il reticolo non emette luce monocromatica, le diffe-
renti lunghezze d’onda che compongono la luce incidente producono massimi prin-
cipali ad angoli diversi, in quanto la (16.11) dipende dalla lunghezza d’onda; solo il
massimo di ordine zero si forma a
q
= 0 per tutte le lunghezze d’onda.
Questa dipendenza dell’angolo di formazione dei massimi dalla lunghezza
d’onda si chiama dispersione angolare, in analogia con la dispersione che si verifi-
ca nella trasmissione attraverso una superficie di discontinuità dell’indice di rifra-
zione, anche se si tratta di fenomeni ben diversi.
Fissato un valore dell’ordine
m
, l’insieme dei massimi che si formano per le
diverse lunghezze d’onda prende il nome di spettro di ordine
m
, per cui si ha uno
spettro del prim’ordine (
m
= 1), uno del secondo ordine (
m
= 2) e così via.
Quando l’illuminazione è in luce bianca, nella quale si trovano con continuità
tutte le lunghezze d’onda comprese tra il viola
l
V
= 0.4
m
m e il rosso
l
R
= 0.7
m
m, lo
spettro
del
prim’ordine
è l’unico cosiddetto
puro
, dato che ad un certo angolo cor-
m
sen
q
0 1 1 2 3 2
l
V
–––
d
l
R
–––
d
Figura 16.25
















