
Reticolo di diffrazione
643
precisa. Tale metodo di produzione di reticoli di grande precisione è stato sviluppa-
to da Rowland verso il 1880.
Esempio 16.7
Un reticolo di diffrazione contiene
N
= 4000 linee su una larghezza
L
= 2 cm; la lar-
ghezza delle fenditure è
a
= 1
m
m. La luce di lunghezza d’onda
l
= 0.5
m
m trasmessa dal
reticolo viene osservata nel piano focale di una lente con
f
= 20 cm. Calcolare la posi-
zione delle frange osservate, la loro larghezza e la loro intensità relativa all’intensità
della frangia centrale.
Soluzione
Il passo del reticolo è
d
=
L
/
N
= 5
m
m e
a
/
d
= 1/5 = 0.2. Per effetto della sola interferen-
za si dovrebbero osservare 20 massimi principali oltre al massimo di ordine zero:
l
sen
q
m
=
m
––– = 0.1
m
,
m
= 0, ± 1, ± 2, … , ± 10 .
d
Invece a causa della diffrazione risulta da (16.13)
R
5
=
R
10
= 0 e
R
6
, … ,
R
9
≤
0.04; per-
tanto in condizioni normali vengono osservati solamente il massimo centrale e gli otto
massimi simmetricamente adiacenti.
Nella tabella sono riportati gli angoli
q
m
ai quali si osservano i massimi, le larghezze
angolari (16.12), le posizioni sullo schermo
z
m
=
f
tg
q
m
, le larghezze
D
z
m
=
f
Dq
delle fran-
ge e le intensità relative
R
m
.
m
sen
q
m
q
m
Dq
z
m
D
z
m
R
m
(gradi)
(rad)
(cm)
(
m
m)
0
0
0
5 · 10
–4
0
10
1
1
0.1
5.74
5.03 · 10
–4
2.01
10.06
0.88
2
0.2
11.54
5.10 · 10
–4
4.08
10.20
0.57
3
0.3
17.46
5.24 · 10
–4
6.29
10.48
0.25
4
0.4
23.58
5.46 · 10
–4
8.73
10.92
0.05
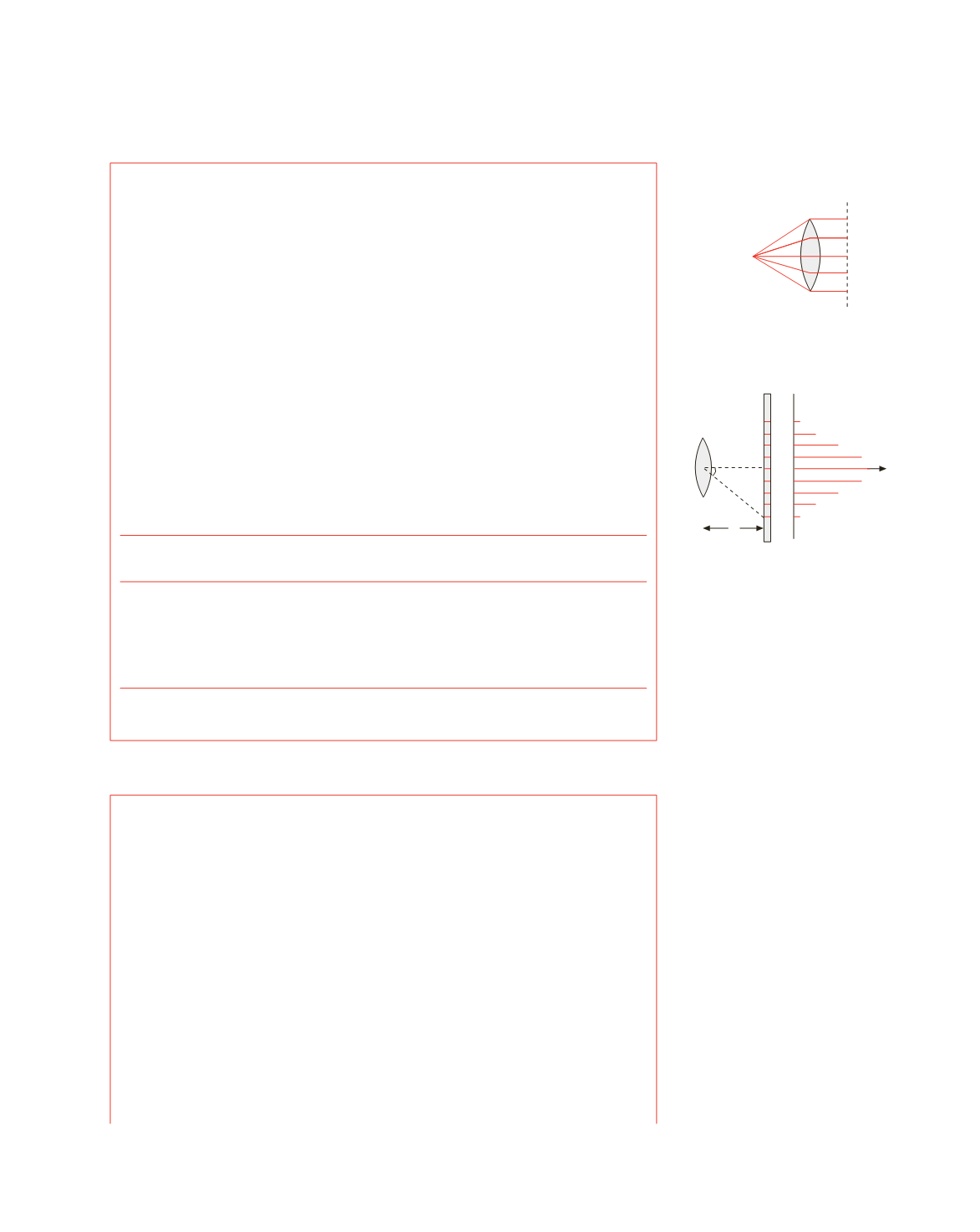
L’immagine è una serie di 9 righe luminose molto sottili (~ 10
m
m), ben distanziate, con
intensità decrescente, su uno sfondo nero.
S
R
m
m
q
4
–4
–2
0
1
2
3
4
f
Figura 16.22
Esempio 16.8
In un esperimento di Young le due fenditure distano
d
= 30
m
m e sono larghe
a
= 3
m
m.
Determinare il numero di frange effettivamente osservabili nell’ipotesi che si riescano a
rivelare solo intensità luminose superiori al 5% dell’intensità della frangia di ordine
zero.
Soluzione
Ponendo
n
= 2 nella (16.10) si ottiene
p
a
sen
q
sen ––––––––
l
p
d
sen
q
I
(
q
) = 4
I
0
[
––––––––––––––
]
2
cos
2
–––––––– ,
p
a
sen
q
l
–––––––––
l
che differisce dalla (15.14) per il termine tra parentesi dovuto alla diffrazione a ciascu-
na delle fenditure. Quando
a
è molto minore di
l
si ha
















