
Reticolo di diffrazione
641
16.5 Reticolo di diffrazione
Nei paragrafi precedenti abbiamo considerato la diffrazione di Fraunhofer pro-
dotta da un’apertura rettangolare o circolare e da un disco opaco. Se disponiamo in
modo regolare
N
fenditure rettilinee, ciascuna di larghezza
a
, equispaziate di una
distanza
d
, realizziamo un sistema di
N
sorgenti, la cui interferenza abbiamo già stu-
diato nel paragrafo 15.5 e nel quale dobbiamo però introdurre il fatto che a causa
della diffrazione l’intensità emessa da ciascuna sorgente ha l’andamento descritto
nel paragrafo 16.2.
Il dispositivo, chiamato
reticolo di diffrazione
, si può realizzare tracciando delle
linee parallele molto sottili su una lastra di vetro per mezzo di un opportuno utensile;
lo spazio che rimane tra una linea e la successiva costituisce una fenditura. La distan-
za
d
tra due fenditure è detta
passo
del reticolo e la larghezza complessiva è
Nd
.
Nella figura 16.20 un’onda piana di lunghezza d’onda
l
incide sul reticolo, che
sta in un piano d’onda (l’incidenza cioè è normale); dopo il reticolo si pone una lente
convergente e si osserva la figura di interferenza nel piano focale della lente. Fissato
un punto
P
sullo schermo, individuato dall’angolo
q
, l’intensità in
P
si calcola con
(15.21), in cui l’intensità
I
1
(
q
) della singola fenditura è data dalla (16.3) che riscri-
viamo:
p
a
sen
q
sen ––––––––
l
I
1
(
q
) =
I
0
[
––––––––––––
]
2
;
p
a
sen
q
–––––––––
l
I
0
è l’intensità a
q
= 0 ed è stato trascurato il contributo del fattore di inclinazione
f
(
q
), non importante per le considerazioni che vogliamo svolgere. Pertanto l’inten-
sità in
P
è
p
a
sen
q
N
p
d
sen
q
sen –––––––– sen ––––––––––
l
l
I
(
q
) =
I
0
[
–––––––––––––
]
2
[
–––––––––––––––
]
2
;
(16.10)
p
a
sen
q
p
d
sen
q
––––––––
sen
––––––––
l
l
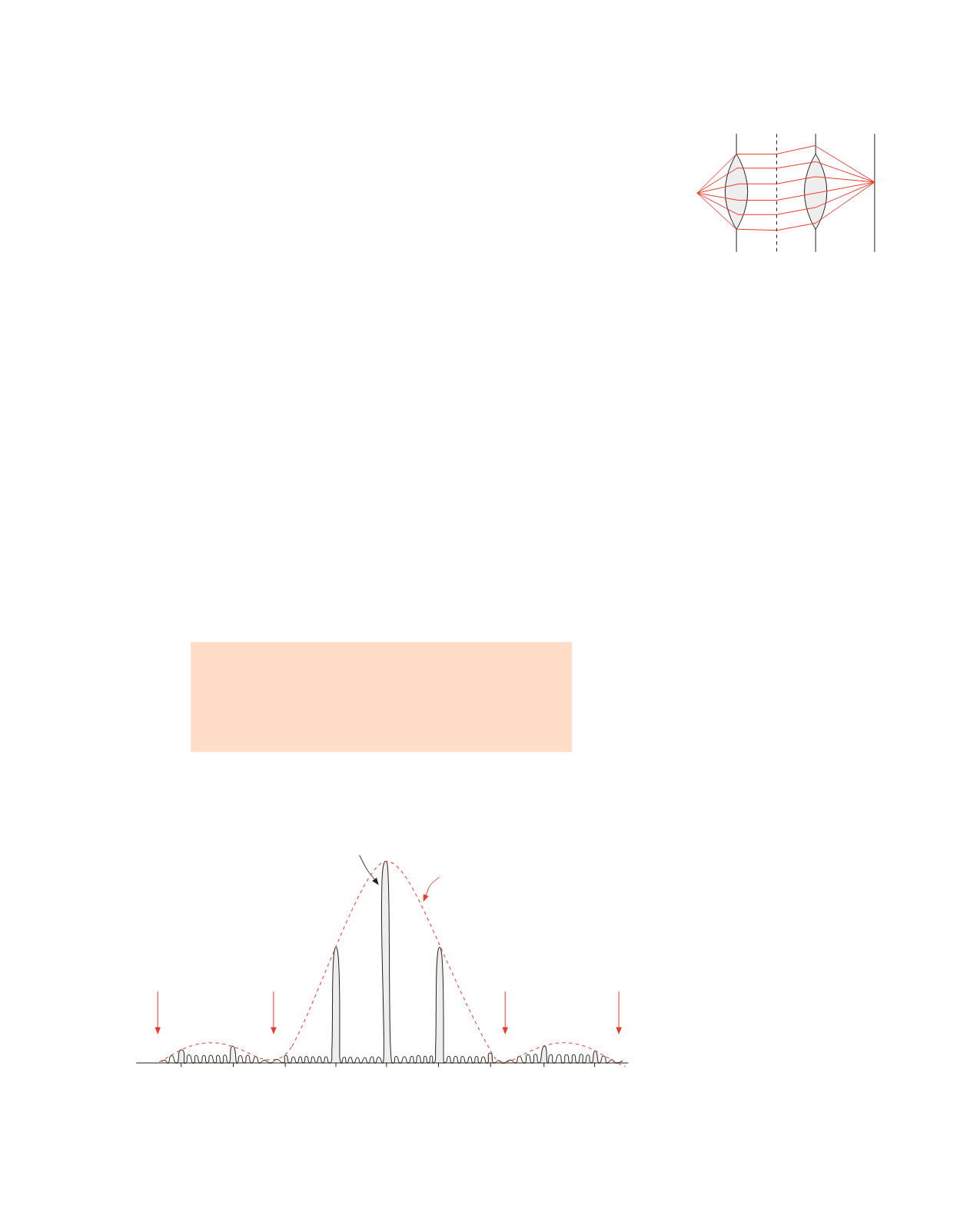
Questa funzione è rappresentata nella figura 16.21 con
N
= 8, come nel terzo caso
della figura 15.27; usualmente si sintetizza il risultato dicendo che l’
intensità della
figura di interferenza è modulata dalla diffrazione.
reticolo
d
P
S
Figura 16.20
Intensità
interferenza
0
C B
A
1
2 3
l
–2 ––
a
l
–4 ––
d
l
–3 ––
d
l
–2 ––
d
l
2 ––
d
l
3 ––
d
l
4 ––
d
l
– ––
d
l
––
d
l
2 ––
a
l
– ––
a
l
––
a
diffrazione
Figura 16.21
















