
638
Diffrazione
ne della direzione
q
= 0, la figura di diffrazione prodotta da un disco opaco di dia-
metro
D
coincide con la figura di diffrazione prodotta da un foro circolare di dia-
metro
D
praticato in uno schermo opaco. Discuteremo nel paragrafo 16.8 cosa suc-
cede per
q
= 0.
16.4 Limite di risoluzione delle lenti
Il fatto che l’immagine di un punto data da una lente sia un un dischetto è impor-
tante quando si vogliano distinguere due oggetti puntiformi, visti dalla lente sotto
un piccolo angolo. La figura 16.15mostra due sorgenti puntiformi incoerenti
S
1
e
S
2
,
molto lontane, viste dalla lente
L
sotto un angolo
a
. Se
a
>>
q
= 1.22
l
/
D
non c’è
sovrapposizione tra i due dischetti che rappresentano le immagini di
S
1
e
S
2
e quindi
le due sorgenti appaiono distinte ovvero, come si dice, risolte. Al diminuire di
a
le
due figure di diffrazione cominciano a sovrapporsi e ad un certo punto diventa
impossibile distinguerle.
Quando
S
1
e
S
2
sono viste dalla lente sotto un angolo
l
a
R
= 1.22 –––
(16.8)
D
il primo minimo della figura di diffrazione di una sorgente coincide con il centro del
massimo dell’altra sorgente e si dice che le due
sorgenti
sono
appena risolte
. Questo
criterio di distinzione è noto come
criterio di Rayleigh
ed è comunemente usato in
ottica; esso è applicabile anche alle immagini date da una fenditura parallela, senza
il fattore 1.22.
L’angolo
a
R
definito da (16.8) si chiama
angolominimo risolvibile
e il suo inver-
so
Esempio 16.5
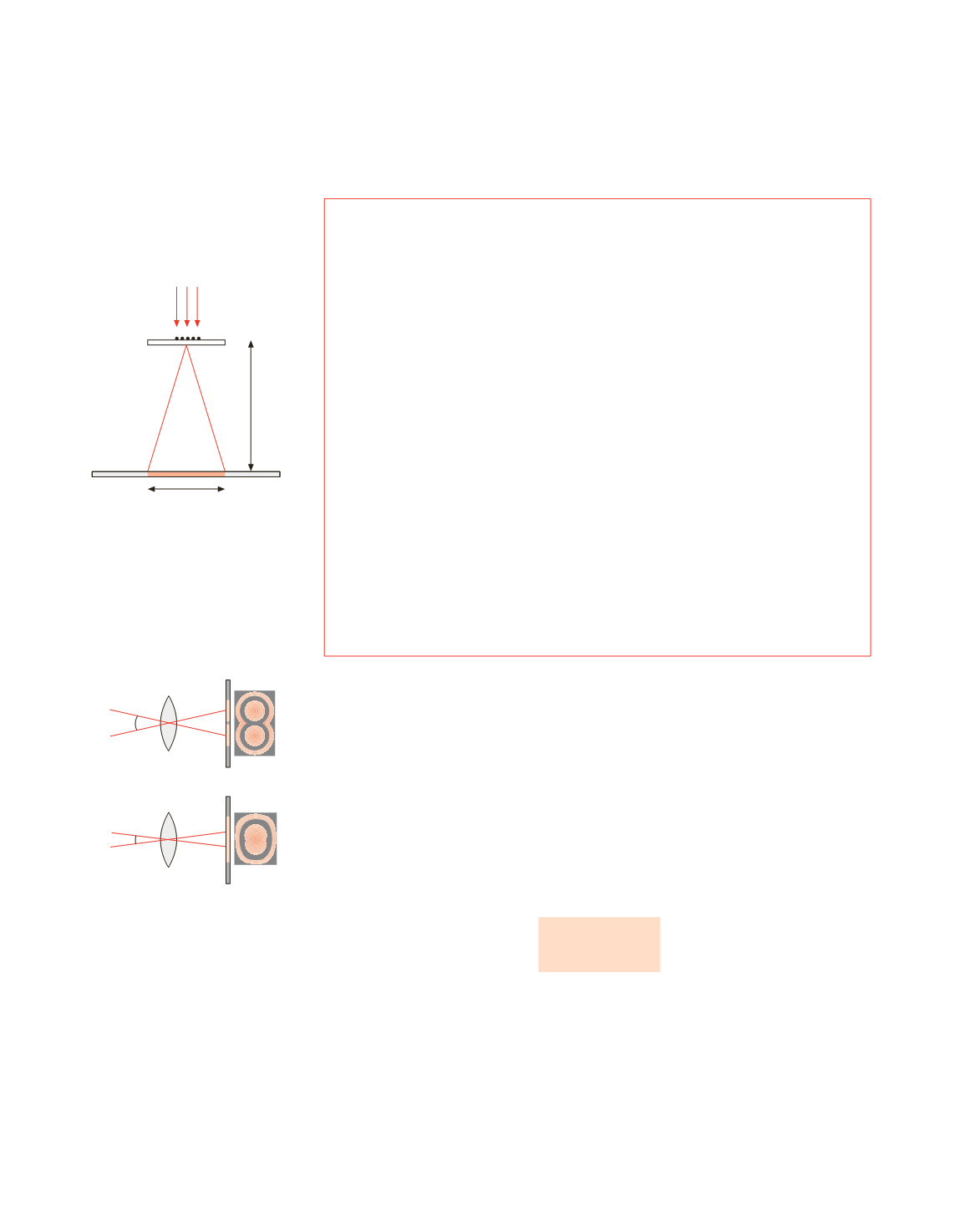
In una ristretta zona di un vetrino è depositato un sottile strato di polvere. Il vetrino è
illuminato con luce rossa di lunghezza d’onda
l
= 0.633
m
m (laser elio-neon). Su uno
schermo
C
posto a distanza
L
= 2 m dal vetrino si osserva un disco rosso di diametro
d
= 15.4 cm. Stimare il diametro
D
dei granelli di polvere.
Soluzione
Ciascun granello può essere schematizzato come un dischetto opaco di diametro
D
e
sullo schermo si osserva la figura di diffrazione. Applichiamo il principio di Babinet e
usiamo le stesse formule dell’esempio 16.4, con
L
al posto di
f
:
L
L
d
= 2.44
l
–––
⇒
D
= 2.44
l
––– = 20
m
m .
D
d
Si vede come la diffrazione possa essere utilizzata per stimare le dimensioni di oggetti
opachi. Perché si possa effettuare la misura deve formarsi il primo minimo, che delimi-
ta l’immagine, e quindi deve essere soddisfatta secondo (16.6) la condizione
l
D
sen
q
= 1.22 –––
≤
1
⇒
l
≤
–––– .
D
1.22
Sono dunque misurabili oggetti di dimensioni confrontabili con la lunghezza d’onda
della luce; se
D
è inferiore a ~5 · 10
–7
m bisogna ricorrere a radiazioni elettromagnetiche
con lunghezza d’onda inferiore, come la radiazione di sincrotrone e i raggi
X
. Vedremo
alcuni esempi nel capitolo 18.
C
d
L
Figura 16.14
a
R
a
S
1
S
2
S
2
S
1
Figura 16.15
Criterio di Rayleigh
















