
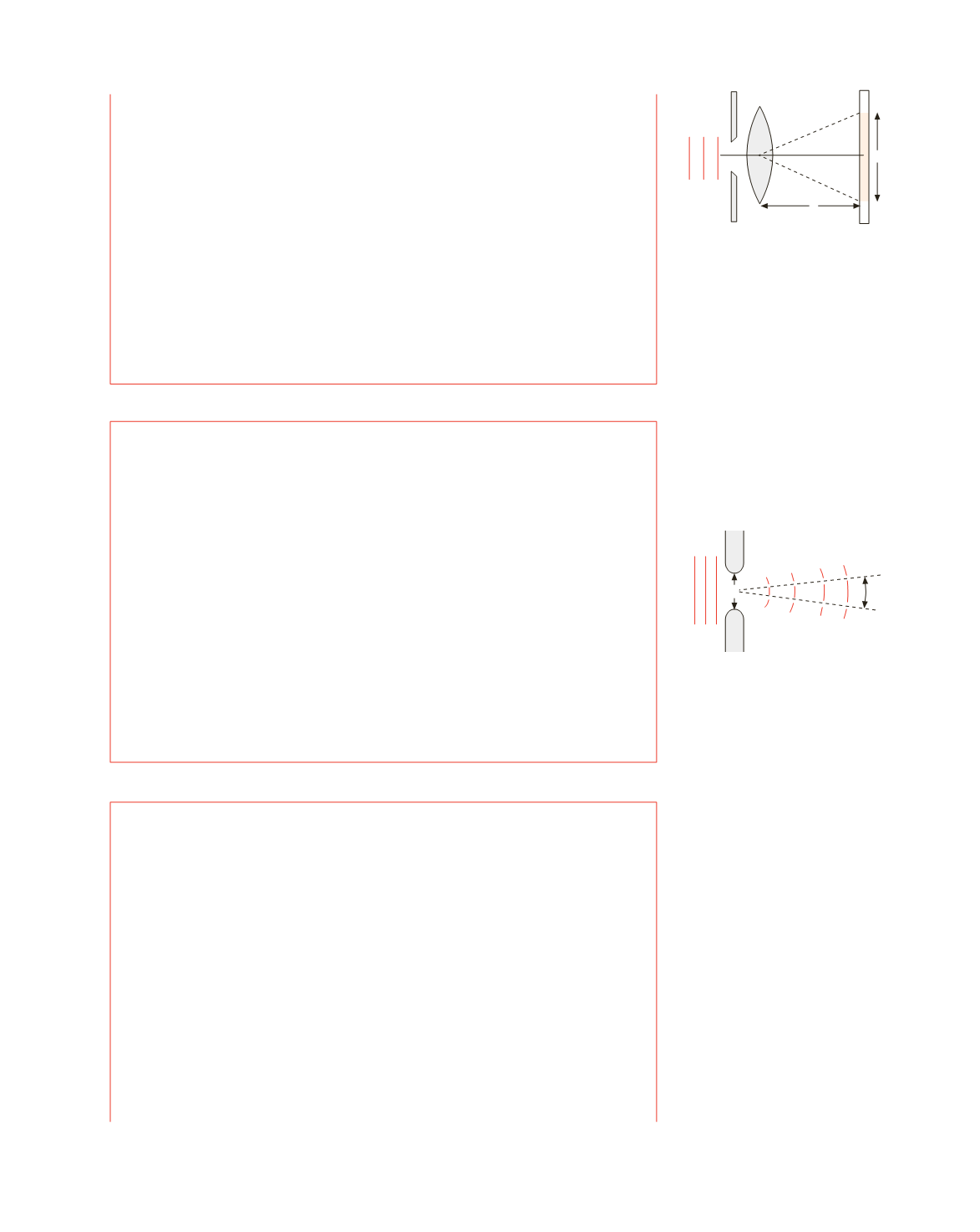
Diffrazione ad una fenditura rettilinea
635
Soluzione
Semilarghezza dell’immagine, distanza focale e angolo
q
a cui si ha il primo minimo
sono legati dalla relazione
D
x
f
tg
q
= ––––
⇒
tg
q
= 6.25 · 10
–3
.
2
Pertanto tg
q
sen
q q
= 6.25 · 10
–3
rad = 0.36° e da (16.4) con
m
= 1
l
––– = 6.25 · 10
–3
,
a
= 0.094 mm
159
l
.
a
È come se, per effetto della diffrazione, la fenditura fosse stata ingrandita del fattore
7.5/0.094 79.
Se volessimo
a
=
D
x
si troverebbe
a
2
= 2
f
l
; con i dati del problema
a
= 0.84 mm: per
tale valori di
a
l’immagine sarebbe larga quanto la fenditura.
D
x
q
f
Figura 16.7
Esempio 16.2
Un piccolo porto è completamente chiuso eccetto che per un’apertura larga
a
= 20 m.
Dall’esterno arrivano in direzione perpendicolare all’apertura onde con lunghezza
d’onda
l
= 1.4 m. Determinare i luoghi dei punti all’interno del porto nei quali il moto
ondoso è minimo.
Soluzione
Applichiamo alle onde marine la trattazione precedente, valida se sono rispettate le stes-
se condizioni geometriche. I minimi di intensità si osservano nelle direzioni date da
(16.4):
l
sen
q
=
m
––– = 0.07
m
,
q
1
= ± 4.0° ,
q
2
= ± 8.0° ,
q
3
= ± 12.1° , … ;
a
il massimo centrale è compreso tra + 4.0° e – 4.0°.
All’interno del porto l’intensità del moto ondoso diminuisce con la distanza dell’aper-
tura in quanto le onde secondarie sono circolari; inoltre l’intensità diminuisce forte-
mente con l’angolo, come si è visto.
a
2
q
1
Figura 16.8
Esempio 16.3
Una fenditura rettilinea larga
a
= 5 · 10
–2
mm è illuminata con luce bianca nella quale
sono presenti con la stessa intensità tutte le lunghezze d’onda dal rosso
l
R
= 0.7 · 10
–3
mm
al violetto
l
V
= 0.4 · 10
–3
mm. La figura di diffrazione si forma su uno schermo posto nel
piano focale di una lente con
f
= 50 cm. Descrivere l’immagine della fenditura.
Soluzione
Il centro dell’immagine è bianco in quanto in esso si realizza la condizione di massimo
di interferenza indipendentemente dalla lunghezza d’onda. Invece la variazione di
intensità sullo schermo e le posizioni dei minimi e dei massimi secondari dipendono
dalla lunghezza d’onda. Dato che in ogni caso
l
<<
a
, si può fare l’approssimazione
sen
q
tg
q q
e scrivere
f
q
=
x
, essendo
x
la posizione sullo schermo in corrisponden-
za all’angolo
q
. Pertanto
p
a
sen
q p
a
q p
a x
p
x
–––––––– –––––– = –––––– = 10
–4
––––
l l
f
l l
















