
636
Diffrazione
16.3 Diffrazione ad un foro circolare e da parte di un disco opaco
Quando l’
apertura
attraverso cui facciamo passare l’onda piana incidente è
cir-
colare
la figura di diffrazione, per ragioni di simmetria, consta di un
disco lumino-
so centrale
circondato da una serie di corone circolari alternativamente scure e chia-
re. Queste frange, osservate in condizioni di Fraunhofer, presentano molte analogie
con quanto visto nel caso dell’apertura rettilinea; lo studio analitico è però più com-
plicato e non lo sviluppiamo.
Si trova in particolare che l’angolo a cui cade il primo minimo di intensità, cor-
rispondente al bordo del disco centrale della figura di diffrazione, è dato da
l
l
sen
q
= 1.22 ––– = 0.61 –––
,
(16.6)
D
R
se
D
e
R
sono rispettivamente il diametro e il raggio del foro circolare. Questa for-
mula va confrontata con la (16.4) che dà, per una fenditura rettilinea larga
a
, sen
q
=
l
/
a
come direzione lungo cui si ha il primo minimo.
Il fattore 1.22 deriva appunto dal calcolo eseguito secondo il principio di Huygens-
Fresnel-Kirchhoff, che integra su tutte le sorgenti secondarie infinitesime anulari in
cui viene suddiviso il foro circolare. Il fattore numerico per il secondo minimo è
2.23, per il terzo 3.24: non si ha una successione regolare come in (16.4).
In molte applicazioni
l
<<
D
e si può scrivere
l l
q
= 1.22 ––– = 0.61 ––– ;
(16.7)
D
R
2
q
è la
larghezza angolare del massimo centrale
.
L’andamento dell’intensità è mostrato in figura 16.11; anche ora si verifica che
oltre l’80% dell’energia trasmessa dall’apertura è concentrata nel disco centrale
luminoso, per cui gli anelli chiari concentrici al massimo centrale non sono ben visi-
bili. Si può dire che il disco centrale, il cui bordo è visto dal centro del foro sotto
l’angolo 2
q
, rappresenta l’immagine del foro stesso.
e la (16.3) si scrive
10
–4
p
x
sen ––––––––
I
l
–––– =
[
–––––––––––––
]
2
.
I
max
10
–4
p
x
––––––––
l
Alle tre lunghezze d’onda
l
V
=0.4 · 10
–3
mm ,
l
G
= 0.55 · 10
–3
mm ,
l
R
= 0.7 · 10
–3
mm ,
il primo minimo si ha per
x
V
= 4.0 mm ,
x
G
= 5.5 mm ,
x
R
= 7.0 mm .
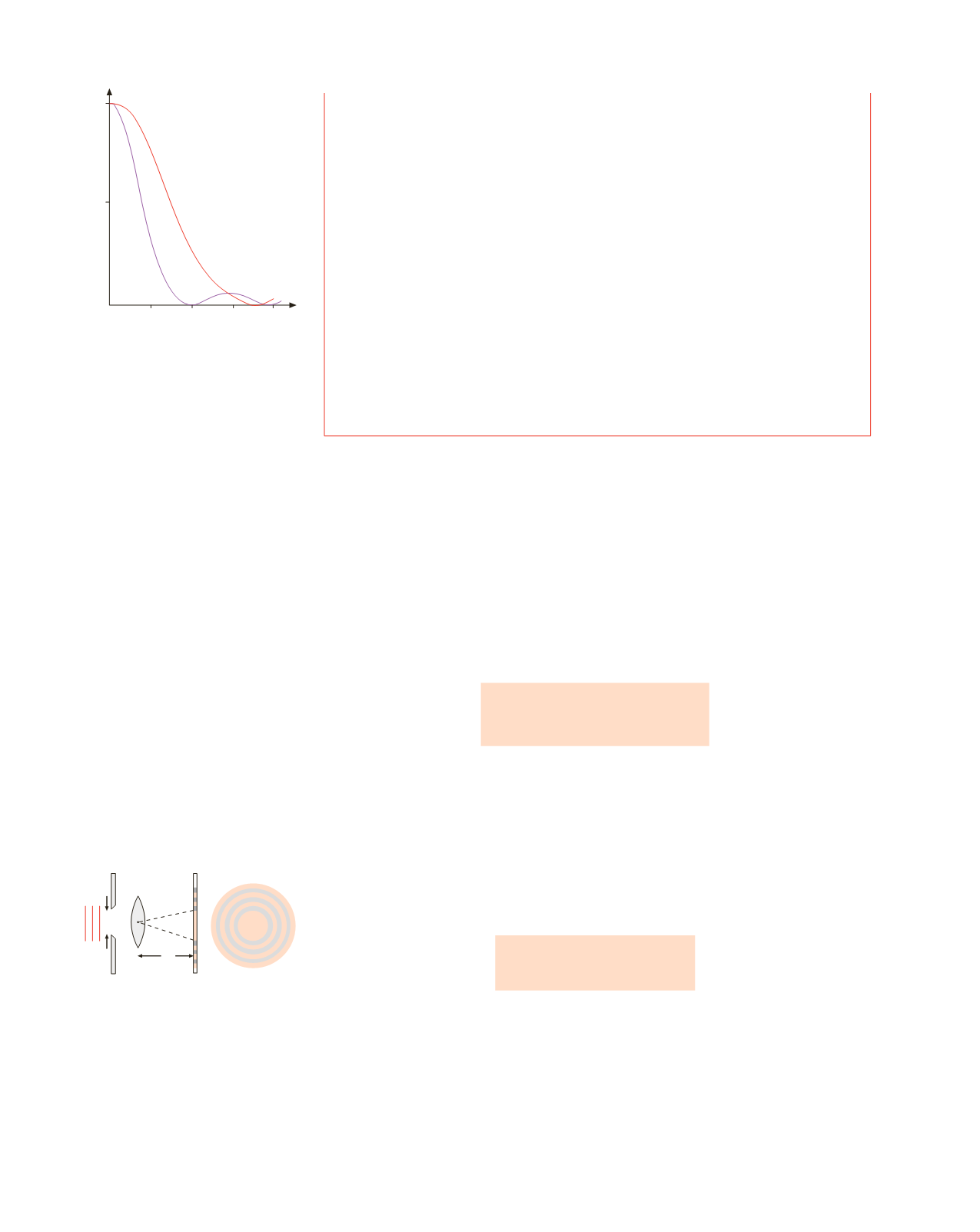
Nella figura 16.9 sono rappresentate le intensità relative per le due lunghezze d’onda
l
V
e
l
R
. Spostandosi dal centro si osserva una colorazione di sottrazione, che va dal rossa-
stro al violaceo, tipica dei fenomeni di interferenza e determinata in ogni punto dalla
mancanza di alcune lunghezze d’onda e dalla presenza più marcata di altre.
I
/
I
max
0.5
2 4 6 8 mm
z
Figura 16.9
Primo minimo di diffrazione
D
f
Figura 16.10
1
















