
Diffrazione ad una fenditura rettilinea
633
15.5), attraverso la costruzione della poligonale degli
N vettori rotanti
rappresen-
tanti le onde che si sovrappongono. Adesso però bisogna far tendere
N
all’infinito
ovvero
D
y
a zero, per cui la poligonale diventa un arco di circonferenza di raggio
r
con angolo al centro
2
p a
= –––
a
sen
q
,
(16.2)
l
eguale alla differenza di fase tra le onde emesse nei punti estremi
A
e
B
della fendi-
tura. Dalla figura 16.4 risulta
a
E
R
= 2
r
sen ––– .
2
La lunghezza dell’arco di circonferenza è
E
max
=
ra
e corrisponde all’ampiezzamas-
sima che si osserva al centro dello schermo, quando
q
= 0 e tutte le onde emesse dalle
singole strisce sono in fase. In definitiva
sen
a
/ 2
E
R
=
f
(
q
)
E
max
–––––––– ,
a
/ 2
espressione nella quale abbiamo evidenziato il fattore di inclinazione
f
(
q
) in quan-
to tutte le ampiezze emesse ad angolo
q
≠
0 vanno moltiplicate per
f
(
q
).
L’intensità è proporzionale al quadrato dell’ampiezza; ricorriamo a (16.2) e
abbiamo
a
p
a
sen
q
sen –––
sen ––––––––
2
l
I
(
q
) =
I
max
f
2
(
q
)
[
––––––––
]
2
=
I
max
f
2
(
q
)
[
––––––––––––
]
2
.
(16.3)
a
p
a
sen
q
–––
–––––––––
2
l
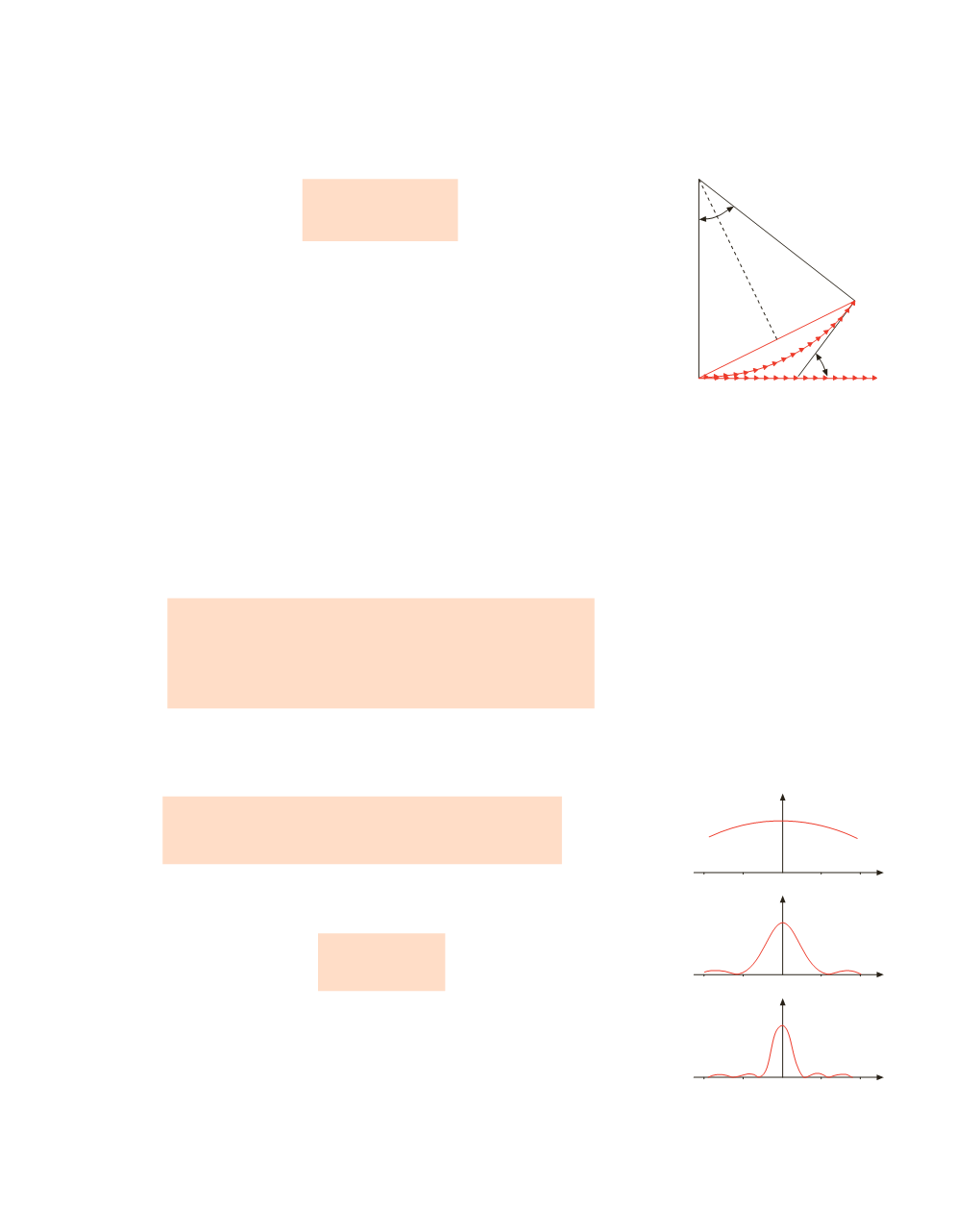
La funzione
I
(
q
) è mostrata in figura 16.5 per i valori
a
= 10
l
,
a
= 5
l
,
a
=
l
.
L’intensità trasmessa dalla fenditura si annulla nei cosiddetti
minimi di diffra-
zione
, quando
p
a
sen
q
l
–––––––– =
m
p
, sen
q
=
m
–––
m
= 1, 2, 3, … .
(16.4)
l
a
I primi minimi, a destra e a sinistra del massimo centrale, si hanno per sen
q
= ±
l
/
a
e la quantità
2
l
D
(sen
q
) = ––––
a
si chiama
larghezza angolare del massimo centrale di diffrazione
. Si vede che per
a
>>
l
il massimo è molto stretto e l’effetto della diffrazione è quasi trascurabile, ma
che il massimo si allarga se
a
diminuisce tendendo a
l
. Se fosse
a
=
l
il primo ed
unico minimo si formerebbe a
q
= 90° e con
a
<
l
l’intensità non si annullerebbe
mai: cioè con
a
≤
l
tutto lo spazio al di là della fenditura è illuminato.
Nella figura 16.6 è ripreso l’andamento di
I
(
q
) in un caso
a
>
l
, insieme ad una
a
r
r
a
E
max
E
R
Figura 16.4
Intensità
Figura 16.5
I
/
I
max
10° 20°
q
10° 20°
q
10° 20°
q
a
=
l
a
= 5
l
a
= 10
l
I
/
I
max
I
/
I
max
















