
634
Diffrazione
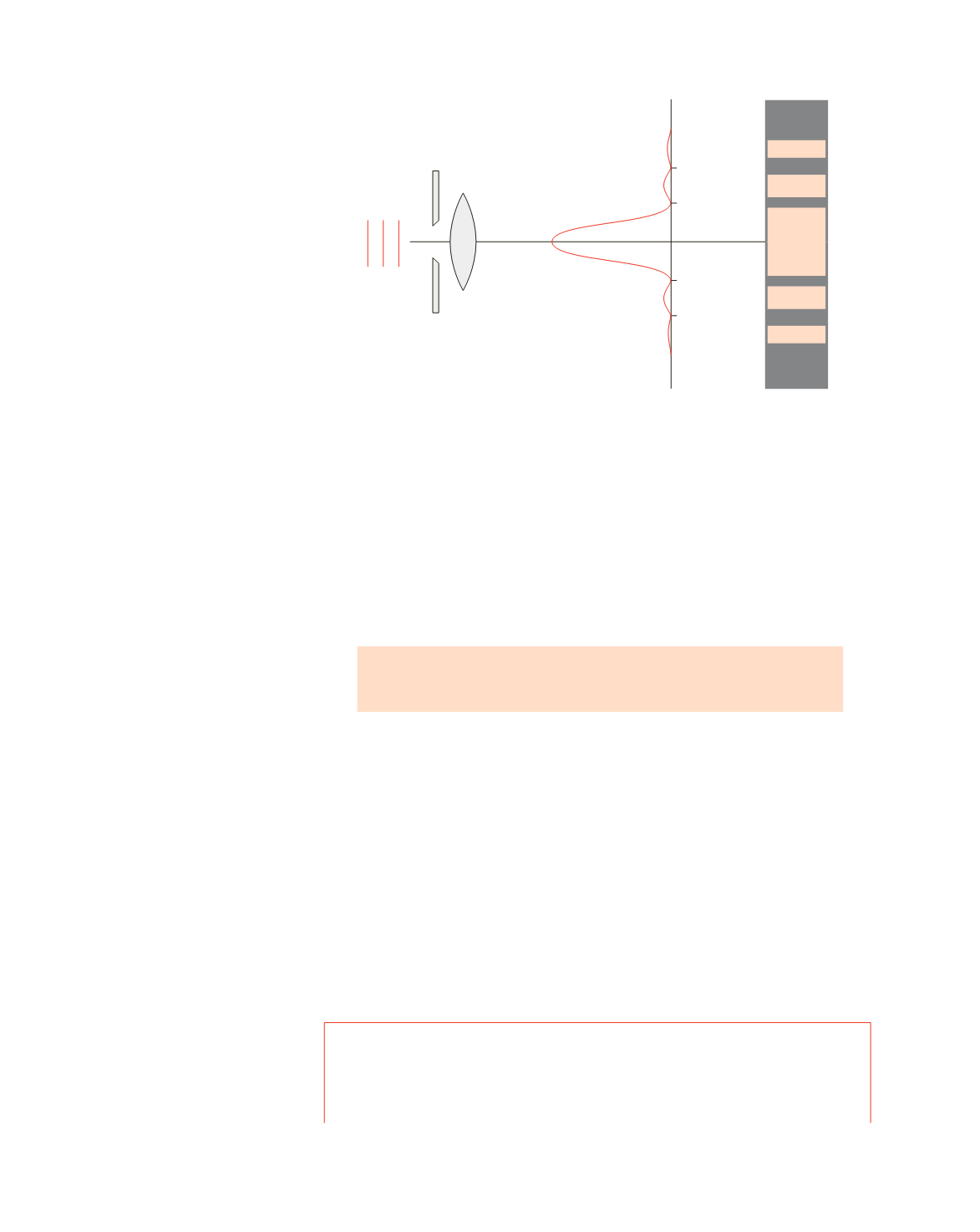
fotografia che mostra l’effetto visivo su uno schermo. Dato che la maggior parte
della potenza (~ 80%) è concentrata nella frangia centrale, si usa dire che questa rap-
presenta l’
immagine della fenditura
.
Tra due minimi d’intensità esiste un
massimo secondario
, la cui posizione si cal-
cola cercando i massimi della funzione (sen
2
b
)/
b
2
, che sintetizza l’andamento
dell’intensità. Si trova la condizione tg
b
=
b
, equazione trascendente risolvibile con
un metodo grafico (a parte il caso ovvio
b
= 0). Risulta però molto buona l’appros-
simazione di considerare massima l’intensità quando è massimo sen
2
(
p
a
sen
q
/
l
),
ovvero quando
p
a
sen
q
p
l
–––––––– = (2
m
' + 1) ––– , sen
q
= (2
m
' + 1) ––––
m
' = 1, 2, 3, … .
l
2
2
a
L’
intensità dei massimi secondari
risulta pertanto, trascurando il fattore di inclina-
zione,
I
m
'
1
0.4
–––– = –––––––––––––– ––––––––– .
I
max
p
(2
m
' + 1)
2
[
(2
m
' + 1) –––
]
2
2
Già nel primo massimo,
m
' = 1, si ha
I
1
/
I
max
= 0.045, ovvero l’intensità è molto
minore rispetto al massimo centrale; per
m
' = 2 il rapporto vale 0.016, per
m
' = 3 vale
0.008 e così via. I rapporti sono ulteriormente depressi se si introduce il fattore
f
2
(
q
). I massimi secondari non sono quindi ben visibili; se
l
non è molto diversa da
a
essi sono abbastanza separati dal massimo centrale e i primi sono percepibili, se
invece
l
<<
a
essi cadono molto vicino alla direzione
q
= 0 e anche per tale ragione
sono praticamente invisibili.
2
l
sen
q
= –––
a
2
l
sen
q
= –––
a
l
sen
q
= –––
a
l
sen
q
= –––
a
Figura 16.6
Esempio 16.1
Un’onda luminosa piana di lunghezza d’onda
l
= 0.59 · 10
–6
m attraversa una fenditura
di larghezza
a
. La larghezza dell’immagine della fenditura, osservata nel piano focale di
una lente di distanza focale
f
= 60 cm, è
D
x
= 7.5 mm. Calcolare il valore di
a
.
















