
632
Diffrazione
L’ampiezza risultante in
P
si ottiene sommando vettorialmente i contributi
dE
pro-
venienti da tutte le sorgenti che costituiscono il foro illuminato, sorgenti che sono
intrinsecamente coerenti, esattamente in fase se la superficie del foro coincide con
una parte del fronte d’onda incidente e con differenza di fase costante negli altri
casi.
Se l’onda incide su un ostacolo opaco, ad esempio un disco, per il calcolo
dell’ampiezza dell’onda in un punto
P
oltre l’ostacolo si procede nello stesso modo,
considerando le parti del fronte d’onda non interessate dall’ostacolo.
Tra i possibili modi con cui si realizza e si osserva la diffrazione prodotta da
aperture e ostacoli illuminati se ne considerano essenzialmente due, legati ai nomi
di Fraunhofer e di Fresnel.
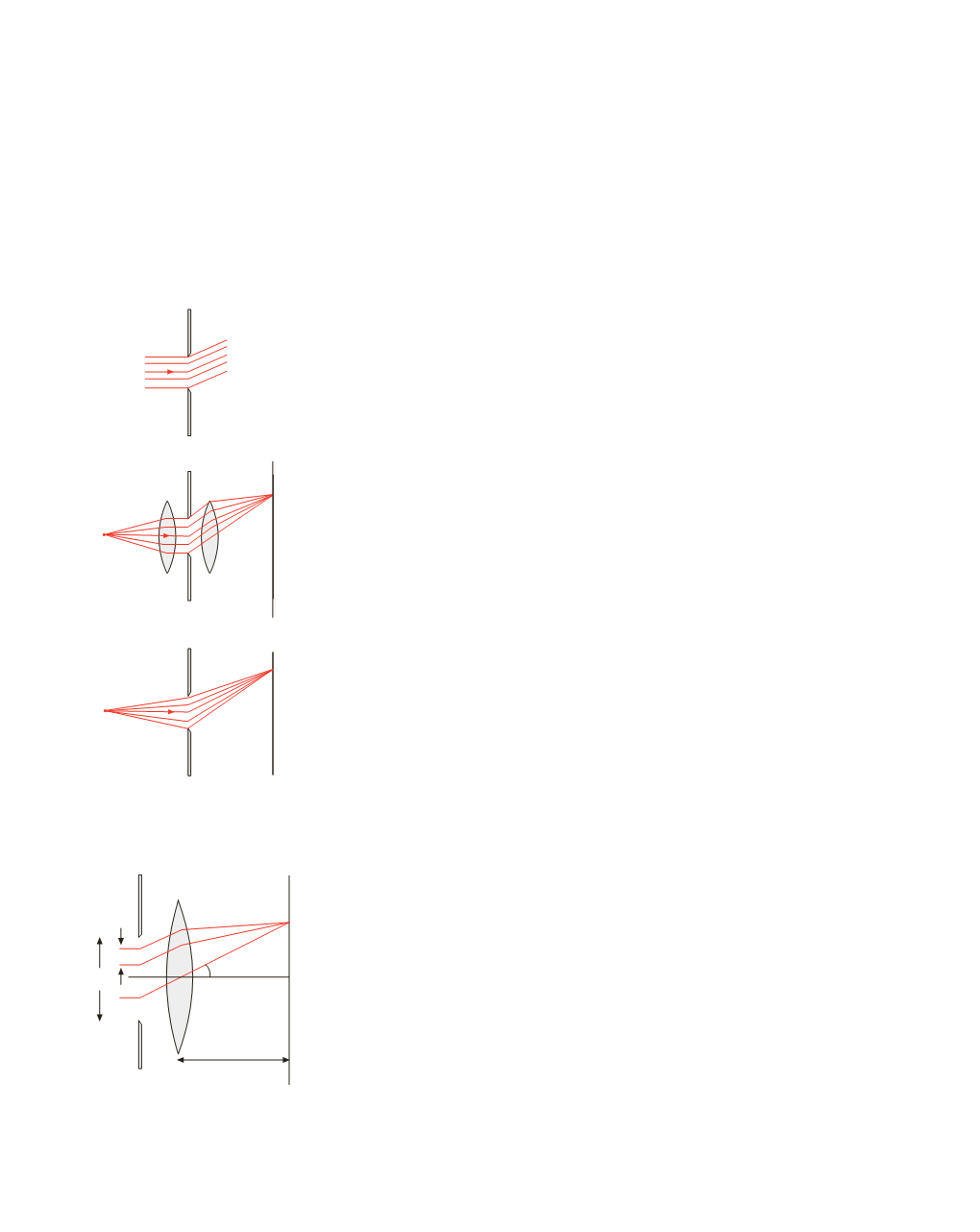
a)
Diffrazione di Fraunhofer
La sorgente di luce
S
e lo schermo
C
sono a grande distanza dall’apertura. I fron-
ti d’onda che giungono su questa sono piani e tali sono anche i fronti d’onda che
giungono in
P
provenienti dall’apertura. Questa configurazione, che è la più sem-
plice da trattare analiticamente, si realizza in laboratorio con due lenti: la prima
L
1
trasforma l’onda sferica proveniente da
S
in un’onda piana con fronte d’onda che
contiene l’apertura, la seconda
L
2
focalizza in un punto
P
i raggi provenienti
dall’apertura secondo una stessa direzione.
b)
Diffrazione di Fresnel
La sorgente
S
e lo schermo
C
sono a distanza finita dall’apertura, i fronti d’onda
non sono piani e i raggi che arrivano in
P
non sono paralleli; la stessa situazione può
essere considerata per un ostacolo generico.
Nel seguito tratteremo per primi i fenomeni di Fraunhofer, che tra l’altro sono
interessanti per le loro implicazioni riguardanti strumenti ottici semplici e compo-
sti. Ci occuperemo successivamente della diffrazione di Fresnel in casi matemati-
camente semplici, ma significativi.
16.2 Diffrazione ad una fenditura rettilinea
Cominciamo a discutere la diffrazione di Fraunhofer considerando un foro ret-
tangolare praticato in uno schermo opaco, di larghezza
a
=
AB
e lunghezza
L
>>
a
,
foro che viene chiamato fenditura rettilinea (indefinita); nella figura 16.3 la fendi-
tura si sviluppa ortogonalmente al disegno.
Supponiamo che sulla fenditura incida un’onda piana di lunghezza d’onda
l
,
con il fronte d’onda parallelo al piano contenente la fenditura, e suddividiamo que-
sta in
N
strisce parallele di larghezza
D
y
. Ciascuna striscia funge da sorgente di onde
secondarie e contribuisce con l’ampiezza
D
E
al campo elettrico risultante
E
R
in un
punto
P
dello schermo individuato dai raggi uscenti ad angolo
q
rispetto alla nor-
male al piano della fenditura. I contributi
D
E
relativi a due strisce adiacenti hanno
nel punto
P
la differenza di fase
2
p Df
= –––
D
y
sen
q
,
l
derivante dalla differenza di cammino
D
y
sen
q
.
Per il calcolo di
E
R
si procede come nel caso di
N
sorgenti coerenti (paragrafo
Fresnel
Fraunhofer
P
C
P
C
L
1
L
2
S
S
S
·
←
∞
∞
Æ
P
Figura 16.2
P
C
B
a
A
f
D
y
q
Figura 16.3
















