
Diffrazione ad un foro circolare e da parte di un disco opaco
637
Questi risultati si applicano chiaramente ad una
lente
di
apertura D
(ovvero di
raggio
R
), per cui l’immagine di una sorgente puntiforme molto lontana è data, nel
piano focale di una lente convergente, da un piccolo disco luminoso le cui dimen-
sioni sono determinate dal rapporto
f
/
D
tra distanza focale e apertura della lente.
Diffrazione da parte di un disco opaco
Consideriamo un’onda piana monocromatica che incide su un’apertura circola-
re
G
di diametro
h
molto maggiore di
l
. A grande distanza, su uno schermo
C
, non
si osserva diffrazione in quanto
h
>>
l
: il campo elettrico
E
G
e l’intensità sono
diversi da zero solo lungo la direzione individuata da
q
= 0, ortogonale al piano di
G
.
Poniamo adesso sull’
apertura G
un
disco opaco A
di diametro
h
avente al cen-
tro un foro circolare di diametro
D
. In un punto
P
dello schermo, visto sotto l’ango-
lo
q
, si osserva un campo elettrico di ampiezza
E
A
(
q
) e un’intensità
I
A
(
q
) propor-
zionale a
E
2
A
(
q
). Se invece di
A
poniamo, nella stessa posizione in cui c’era il foro
di
A
, un
disco opaco B
di diametro
D
, nel punto
P
si osservano un campo elettrico di
ampiezza
E
B
(
q
) e un’intensità
I
B
(
q
) proporzionale a
E
2
B
(
q
); la luce raggiunge lo
schermo passando attraverso un’apertura anulare compresa tra il raggio
D
/2 e il rag-
gio
h
/ 2.
Notiamo che le
aperture
costituite dal foro nel disco
A
e dall’anello dovuto alla
presenza del disco
B
sono
complementari
, ossia non hanno nessuna zona in comu-
ne: se sovrapponiamo i loro effetti è come se ci fosse soltanto l’apertura
G
. Pertanto
E
G
(
q
) =
E
A
(
q
) +
E
B
(
q
) ;
d’altra parte
E
G
(
q
) = 0 per
q
≠
0 e concludiamo che
E
B
(
q
) = –
E
A
(
q
) ,
I
B
(
q
) =
I
A
(
q
) per
q
≠
0 .
Questo risultato, noto come
principio di Babinet
, stabilisce che, con l’esclusio-
I
(
q
)
1
0.5
sen
q
l
1.22 ––
D
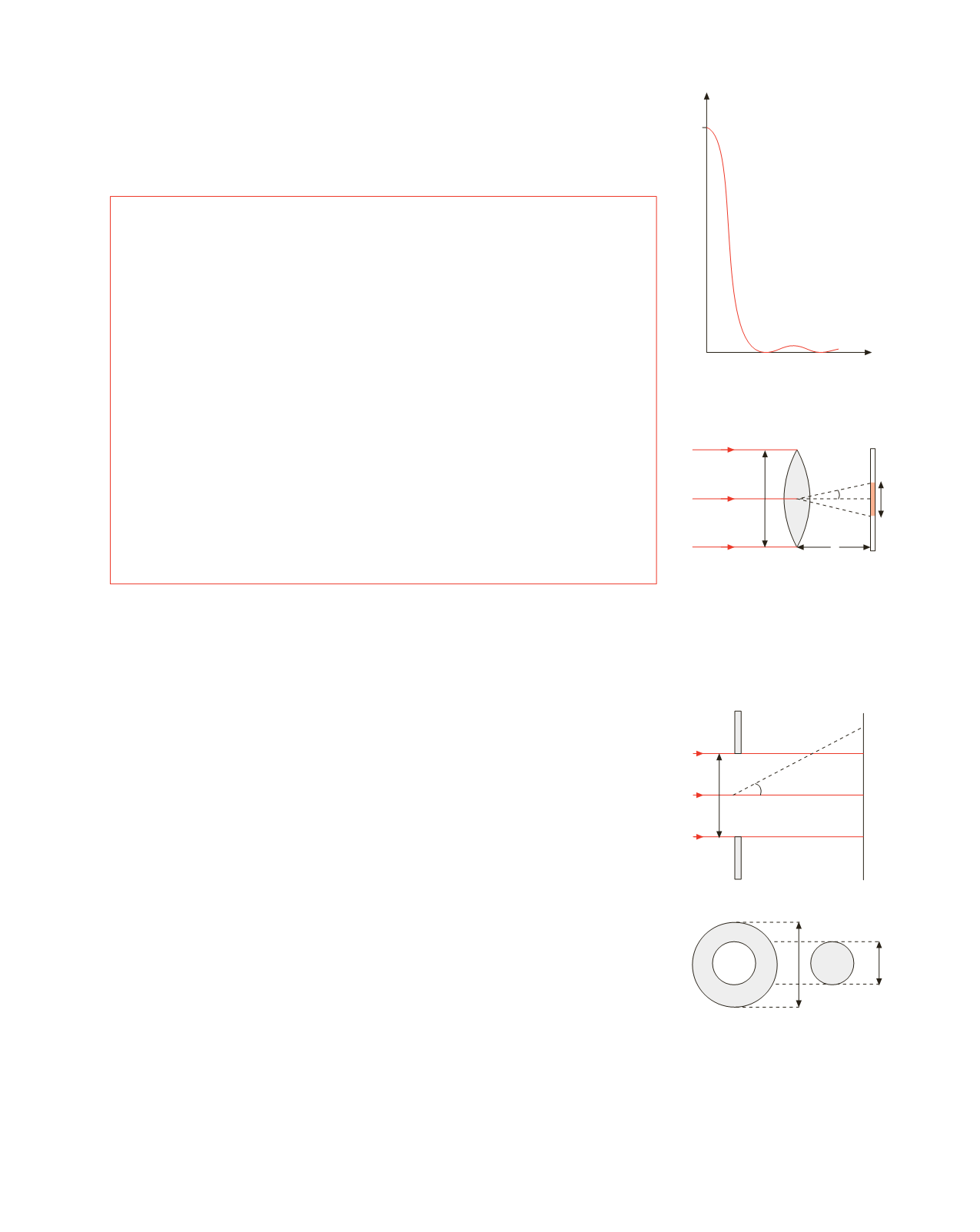
Figura 16.11
Esempio 16.4
L’obiettivo di una macchina fotografica, di apertura
D
=2.5 cm e distanza focale
f
= 5
cm, è illuminato da una sorgente puntiforme lontana
S
, che emette luce di lunghezza
d’onda
l
= 0.55
m
m. Calcolare le dimensioni dell’immagine
S
nel piano focale
dell’obiettivo.
Soluzione
Siamo di sicuro nella condizione
l
<<
D
e utilizziamo (16.7): l’apertura angolare 2
q
dell’immagine vista dal centro della lente è
l
2
q
= 2.44 ––– = 5.37 · 10
–5
rad .
D
L’immagine di
S
è un dischetto di diametro
f
d
= 2
q
f
= 2.44
l
––– = 2.68
m
m .
D
A causa della diffrazione il fuoco non è un punto geometrico, bensì acquista una dimen-
sione finita, per quanto piccola e in molte applicazioni trascurabile.
D
q
d
f
Figura 16.12
P
G
h
h
A
B
D
q
Figura 16.13
Principio di Babinet
















