
Limite di risoluzione delle lenti
639
1
D
r
= ––– = –––––––
(16.9)
a
R
1.22
l
è detto
potere risolutivo
o
separatore della lente
.
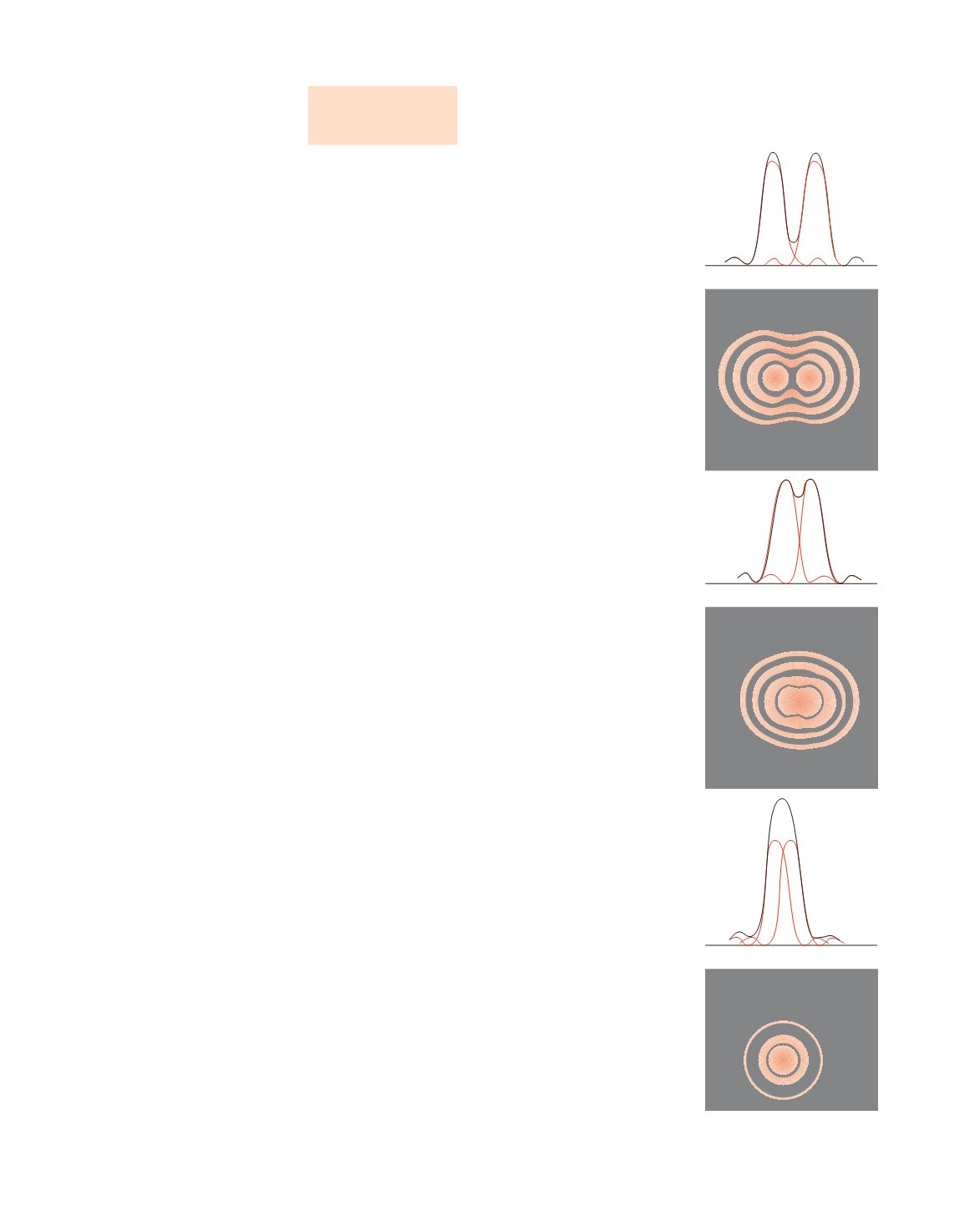
In figura 16.16 sono rappresentate le figure di diffrazione prodotte separata-
mente dalle due sorgenti in varie situazioni angolari:
a
>
a
R
curve risolte,
a
=
a
R
curve appena risolte,
a
<
a
R
curve non risolte. La linea tratteggiata mostra l’intensità
totale, ottenuta come somma dei due contributi.
Nel capitolo 17 descriveremo il funzionamento di alcuni strumenti ottici fonda-
mentali, quali il telescopio, il microscopio e lo stesso occhio umano. Un aspetto
qualificante è la capacità di separare, cioè di osservare come distinti, due punti lumi-
nosi separati, siano essi due stelle o due parti di una piccola struttura. Una conse-
guenza della discussione svolta finora è che una delle principali cause che limita la
risoluzione di una lente è la diffrazione, fatto intrinseco in quanto legato alla natura
ondulatoria della luce e quindi non eliminabile.
Esaminiamo adesso il potere separatore per i tre strumenti suddetti, considerati
come semplici lenti di apertura
D
e focale
f
.
Potere separatore di un telescopio
Il potere separatore (16.9) non dipende dalla distanza focale della lente, ma soltanto dalla
sua apertura, e migliora al crescere di questa.
La stessa formula è valida quando il fascio luminoso, invece di essere rifratto da una
lente, è riflesso da uno specchio sferico di apertura
D
e focale
f
. Il maggior telescopio ottico
a riflessione del mondo, situato sul Monte Palomar negli USA, ha
D
= 5 m: con
l
= 0.589 ·
10
–6
m
1
a
R
= 1.44 · 10
–7
rad 0.03” ,
r
= ––– = 6.95 · 10
6
rad
–1
.
a
R
Sia
a
R
che
r
dipendono dalla lunghezza d’onda, essendo peggiori le prestazioni con luce rossa
e migliori con luce violetta:
l
R
= 0.7 · 10
–6
m ,
a
R
= 1.71 · 10
–7
rad ,
r
= 5.85 · 10
6
rad
–1
,
l
V
= 0.4 · 10
–6
m ,
a
R
= 0.98 · 10
–7
rad ,
r
= 1.03 · 10
7
rad
–1
.
Potere separatore di un microscopio
In un microscopio invece della separazione angolare è più conveniente specificare la
distanza minima
s
tra due punti distinguibili. Se i due punti sono nel piano focale anteriore
dell’obiettivo (vedi paragrafo 17.8), essi sono visti sotto l’angolo
q
=
s
/
f
; utilizzando per
q
il valore numerico
a
R
otteniamo
f
f
s
=
f
a
R
= 1.22
l
––– = 0.61
l
––– .
D
R
Questa relazione viene scritta di solito in funzione dell’
angolo
f
di
accettanza
dell’obiettivo,
definito da sen
f
=
R
/
f
, per cui
0.61
l
0.61
l
0
s
= ––––––– = –––––––– ,
sen
f
n
sen
f
dove l’ultimo passaggio tiene conto della possibilità che l’oggetto e la parte frontale dello
strumento siano immersi in un mezzo con indice di rifrazione
n
;
l
è la lunghezza d’onda in
questo mezzo e
l
0
la lunghezza d’onda nel vuoto della luce usata per illuminare l’oggetto. Il
a
>
a
R
a
=
a
R
a
<
a
R
Figura 16.16
Potere risolutivo
















