
652
Diffrazione
Lo stesso risultato si ottiene anche scrivendo
1 1
1
1
E
P
=
E
1
–
E
2
+
E
3
–
E
4
+ … = ––
E
1
+ –– (
E
1
– 2
E
2
+
E
3
) + –– (
E
3
– 2
E
4
+
E
5
) + … = ––
E
1
.
2 2
2
2
I segni più e meno alternati sono dovuti alle successive differenze di fase di
p
e i termini tra
parentesi si considerano nulli in quanto si ammette che per effetto dell’interferenza il contri-
buto di ciascuna zona di Fresnel con
n
pari sia compensato dai contributi delle due semizone
dispari adiacenti.
Diffrazione di un foro circolare
Per quanto detto è evidente che, fissato un punto
P
distante
r
0
dal piano d’onda, ad ogni
disco di raggio
R
(0
≤
R
<
∞
) tracciato sul piano come in figura 16.33 è associato, sulla curva
a spirale dei vettori rotanti un punto
O
", ovvero un vettore
OO
" la cui ampiezza dà l’ampiez-
za del campo elettrico
E
P
prodotto in
P
dalla porzione del fronte d’onda coincidente col disco.
Quando
R
eguaglia il raggio di una delle zone di Fresnel il punto
O
" sta sulla verticale pas-
sante per
O
.
Il ragionamento svolto finora può apparire puramente formale; se ne scopre però l’utilità
non appena si interpone sul fronte d’onda, a distanza
r
0
da
P
, uno schermo opaco con un foro
di raggio
R
:
OO
" dà l’ampiezza del campo elettrico trasmesso dal foro e l’intensità
I
P
è pro-
porzionale a (
OO
")
2
. Facendo variare con continuità
R
da zero a infinito si ottiene per
I
P
l’andamento mostrato in figura 16.36: a causa dell’interferenza tra le varie porzioni del fron-
te d’onda l’intensità dipende fortemente dal raggio del foro. I punti di
massima intensità
si
hanno quando il foro comprende esattamente un
numero dispari di zone di Fresnel
, cioè per
raggi
R
pari a
R
1
=
r
0
l
,
R
3
= 3
R
1
,
R
5
=
5
R
1
, … secondo (16.16); i punti di
minima
intensità
si osservano invece con i raggi
R
2
= 2
R
1
,
R
4
= 2
R
1
,
R
6
= 6
R
1
, …, cioè quan-
do il foro ricopre esattamente un
numero pari di zone di Fresnel
; la linea tratteggiata rappre-
senta l’intensità in assenza dello schermo col foro. I valori dei massimi sono decrescenti e
quelli dei minimi crescenti perché le ampiezze dei campi decrescono all’aumentare di
R
:
E
1
>
E
1
–
E
2
+
E
3
>
E
1
–
E
2
+
E
3
–
E
4
+
E
5
> … ,
E
1
–
E
2
<
E
1
–
E
2
+
E
3
–
E
4
< … .
Quanto discusso avviene sull’asse del foro. Per determinare l’intensità in un punto
Q
che
non sta sull’asse
OP
occorre tener presente che il sistema di zone di Fresnel è caratteristico
del punto di osservazione: spostandosi da
P
a
Q
parallelamente al piano del foro le zone di
Fresnel si spostano rigidamente con
Q
. In una generica posizione l’ampiezza
E
Q
risulta dalla
sovrapposizione dei campi di quelle porzioni di zone intersecate dal foro (figura 16.37).
Anche quando il punto
Q
è nella zona d’ombra geometrica in esso si osserva un’intensità non
nulla.
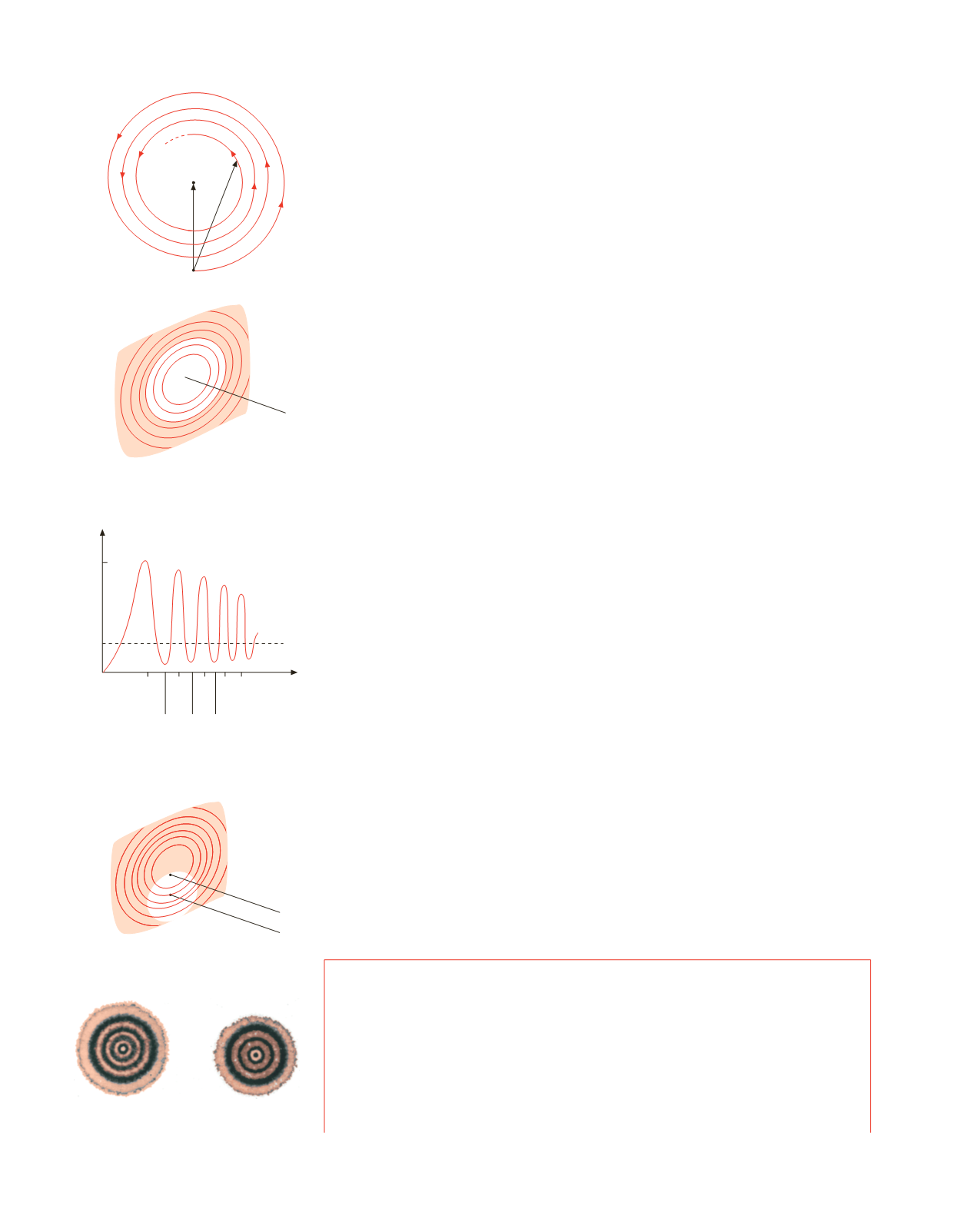
La figura di diffrazione completa osservata sullo schermo distante
r
0
dal foro consta di
una serie di corone circolari alternativamente chiare e scure, con il centro chiaro se
R
=
R
1
,
R
3
,
R
5
, …, scuro se
R
=
R
2
,
R
4
,
R
6
, … . Due esempi sono mostrati in figura 16.38.
Supponiamo ora di cambiare la distanza
r
0
mantenendo costanti la lunghezza d’onda
l
e
il raggio
R
del foro. Ad ogni valore di
r
0
è associato un sistema d’azione di Fresnel in quanto
i raggi delle zone dipendono da
r
0
secondo (16.16); ci sono valori di
r
0
per i quali nel foro
cadono un numero dispari di zone e valori per i quali invece le zone coincidenti col foro sono
in numero pari: ai primi valori corrispondono massimi di intensità sull’asse, ai secondi mini-
mi di intensità. Trattiamo numericamente questa situazione nel successivo esempio.
O
'
O
"
O
r
0
P
E
P
=
E
1
–
E
2
+
E
3
Figura 16.35
I
P
R
1
R
2
R
4
R
6
R
3
R
5
R
7
R
9
R
I
1
I
1
––
4
Figura 16.36
O
'
O
r
0
r
0
Q
P
Figura 16.37
Figura 16.38
Esempio 16.11
Un’onda piana monocromatica di lunghezza d’onda
l
= 0.685
m
m incide su un’apertura
circolare di raggio
R
= 2 mm. Determinare a quali distanze lungo l’asse del foro si osser-
vano massimi di intensità e a quali distanze minimi di intensità.
Soluzione
Fissato un punto
P
sull’asse del foro a distanza
r
0
, costruiamo il corrispondente sistema
di zone di Fresnel. Se
r
0
è tale che
R
2
=
r
0
l
, il foro corrisponde alla prima zona di
















