
654
Diffrazione
sata la distanza
r
0
che corrisponde a questo sistema di zone. Un’onda piana monocromatica
incidente con quella data
l
viene in parte concentrata nel punto
P
distante
r
0
dal centro del
reticolo zonato e quindi possiamo considerare che questo si comporti come una
lente con-
vergente
di focale
R
2
1
R
2
n
f
=
r
0
= –––– = –––– .
(16.17)
l
n
l
Sappiamo che per una distanza
r
<
r
0
i raggi delle zone di Fresnel relative a
r
sono inferiori ai
raggi delle corrispondenti zone relative a
r
0
. Quindi esiste una distanza
r
<
r
0
tale che in una
corona circolare trasparente del reticolo zonato cadano tre zone di Fresnel invece che una,
oppure cinque o sette o in generale un numero dispari di zone maggiore di uno. Per tutte le
distanze che soddisfano a questa condizione abbiamo un massimo secondario di intensità: a
differenza della lente che dà una sola immagine il reticolo zonato ne può dare molte.
Diffrazione di un disco opaco
Consideriamo ora la diffrazione subita da un’onda piana di lunghezza d’onda
l
che inci-
de ortogonalmente su un disco opaco di raggio
R
, osservando cosa succede in un punto
P
posto a distanza
r
0
dal disco.
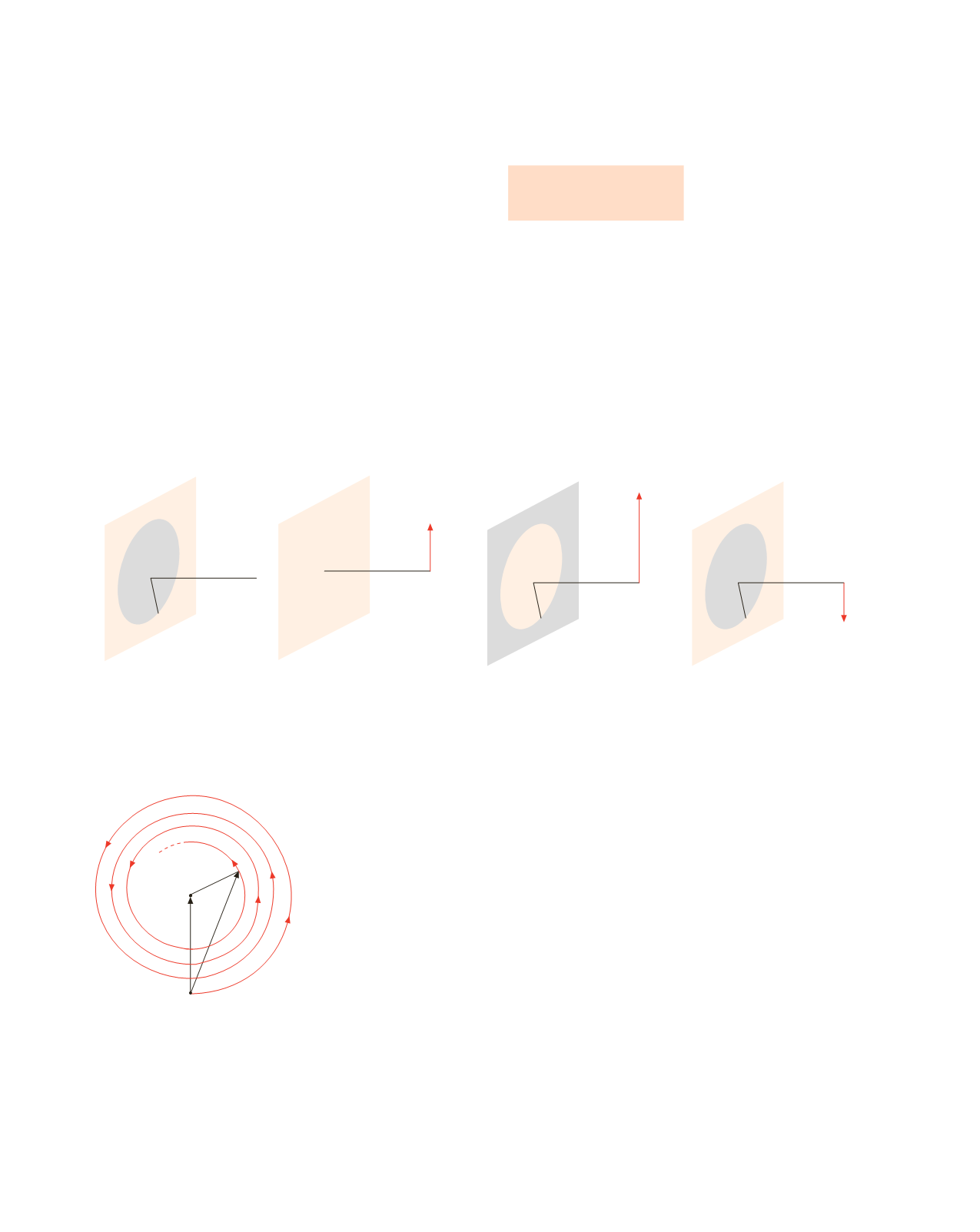
Il campo elettrico
E
disco
dell’onda diffratta si ottiene utilizzando il principio di sovrappo-
sizione schematizzato in figura 16.41. Detto
E
il campo elettrico nella situazione senza osta-
coli, si può porre
E
=
E
disco
+
E
foro
⇒
E
disco
=
E
–
E
foro
.
Ricordiamo che
E
=
E
1
/ 2, rappresentato dal vettore
OO
', e che
E
foro
è rappresentato da
OO
"; seguendo la figura 16.42 deduciamo che
E
disco
è rappresentato da
O"O'
.
All’aumentare del raggio
R O
" tende a
O
', l’intensità
I
disco
, proporzionale a (
O
'
O
")
2
, tende
a zero, restando però sempre diversa da zero per dimensioni finite. Quindi in
P
, indipenden-
temente dal raggio del disco, si osserva sempre un punto luminoso.
Tale punto luminoso situato dietro un ostacolo era stato osservato per la prima volta da
Maraldi verso il 1700, ma il fatto venne dimenticato. Quando Fresnel nel 1818 presentò la sua
teoria della diffrazione, sostenendo quindi la natura ondulatoria della luce, Poisson dedusse
matematicamente che, se la teoria era vera, doveva esserci un punto luminoso dietro un osta-
colo opaco e concluse che la teoria era inverosimile. Invece Arago eseguì l’esperimento,
ritrovò il punto luminoso di Maraldi e confermò la validità delle ipotesi di Fresnel. Per ironia
della sorte il punto luminoso in questione è chiamato
punto luminoso di Poisson
.
fronte d’onda
R
P
r
0
r
0
P
P
P
R
r
0
R
r
0
E
E
=
E
foro
+
E
disco
E
foro
E
disco
Figura 16.41
O
'
O
"
O
OO
' =
E
,
OO
" =
E
foro
O
"
O
' =
E
disco
Figura 16.42
















