
660
Diffrazione
Un dispositivo per l’osservazione della diffrazione di raggi
X
è lo
spettrografo a cristal-
lo
della figura 16.54, ideato da Bragg. In corrispondenza ad una determinata serie di piani
reticolari, cioè ad un certo valore di
d
, si varia l’angolo
q
e misurando gli angoli dei massimi
si deduce dalla (16.19) lo spettro delle lunghezze d’onda del fascio di raggi
X
. Si verifica così
l’esistenza della componente continua alla radiazione di frenamento, alla quale è sovrappo-
sta la componente a
righe
caratteristica della struttura atomica del materiale emettitore. In
figura 16.55 è mostrato uno dei primi spettri ottenuti da Bragg nel 1913: sono visibili gli spet-
tri del primo e del second’ordine, ciascuno con tre righe. Viceversa, utilizzando un fascio
monocromatico di raggi
X
si possono determinare le varie distanze
d
, acquisendo informa-
zioni sulla struttura cristallina del materiale usato come bersaglio nello spettrografo.
Se il fascio incidente può incontrare nel cristallo diverse famiglie di piani reticolari
l’aspetto della figura di diffrazione è molto diverso. In effetti la prima evidenza sperimenta-
le sulla natura ondulatoria dei raggi
X
venne ottenuta da von Laue nel 1912, con l’apparato
schematizzato in figura 16.56. Un fascio di raggi
X
con piccola sezione incide su un sottile
cristallo di solfuro di zinco; su una lastra fotografica si osserva la figura di diffrazione. Questa
consta di un insieme di punti disposti in modo regolare intorno al fascio centrale trasmesso;
ciascun punto è la traccia di una direzione lungo cui si è avuto un massimo. Infatti una lun-
ghezza d’onda
l
incidente può trovare una coppia di valori
d
i
e
q
i
per i quali è soddisfatta
(16.19) con un certo valore intero positivo
m
i
: vuol dire che la direzione di incidenza forma
l’angolo di radenza
q
i
con una famiglia di piani reticolari aventi tra loro distanza
d
i
e che 2
d
i
sen
q
i
=
m
i
l
; il raggio diffratto impressiona la lastra in una zona ristretta, quasi puntiforme.
Data
l
la (16.19) può essere soddisfatta anche per una terna di valori
d,
q
, m
diversa dalla pre-
cedente e il fatto si può ripetere per le altre lunghezze d’onda incidenti. Si forma così lo
spet-
trogramma a punti di Laue
nel quale ad ogni punto è dunque associata una famiglia di piani
reticolari; esso è caratteristico della struttura cristallina illuminata col fascio di raggi
X
.
Invece che da un cristallo supponiamo che il materiale diffondente sia costituito da una
polvere contenente un gran numero di microcristalli, orientati in maniera casuale. Se la con-
dizione (16.19) è soddisfatta per una data famiglia di piani reticolari di un particolare micro-
cristallo, essa viene soddisfatta anche da moltissimi altri microcristalli e al posto di un punto
abbiamo sulla lastra fotografica una circonferenza. È come prendere una particolare situa-
zione realizzata col metodo di Laue e ruotare il cristallo attorno all’asse del fascio: infatti
nella polvere cristallina si trovano tutte le orientazioni che corrisponderebbero ad una tale
rotazione. Lo
spettrogramma
, detto di
Debye-Scherrer
, contiene una serie di circonferenze,
ognuna generata come descritto con una diversa famiglia di piani reticolari.
La diffrazione dei raggi
X
, oltre che per la spettroscopia dei raggi
X
stessi e per indagini
sui cristalli, è utilizzato anche per lo studio di strutture microscopiche come quelle di mole-
cole biologiche complesse, tipo DNA.
rivelatore
2
q
q
cristallo
intensità
+
e
Figura 16.54
10°
20°
q
Figura 16.55
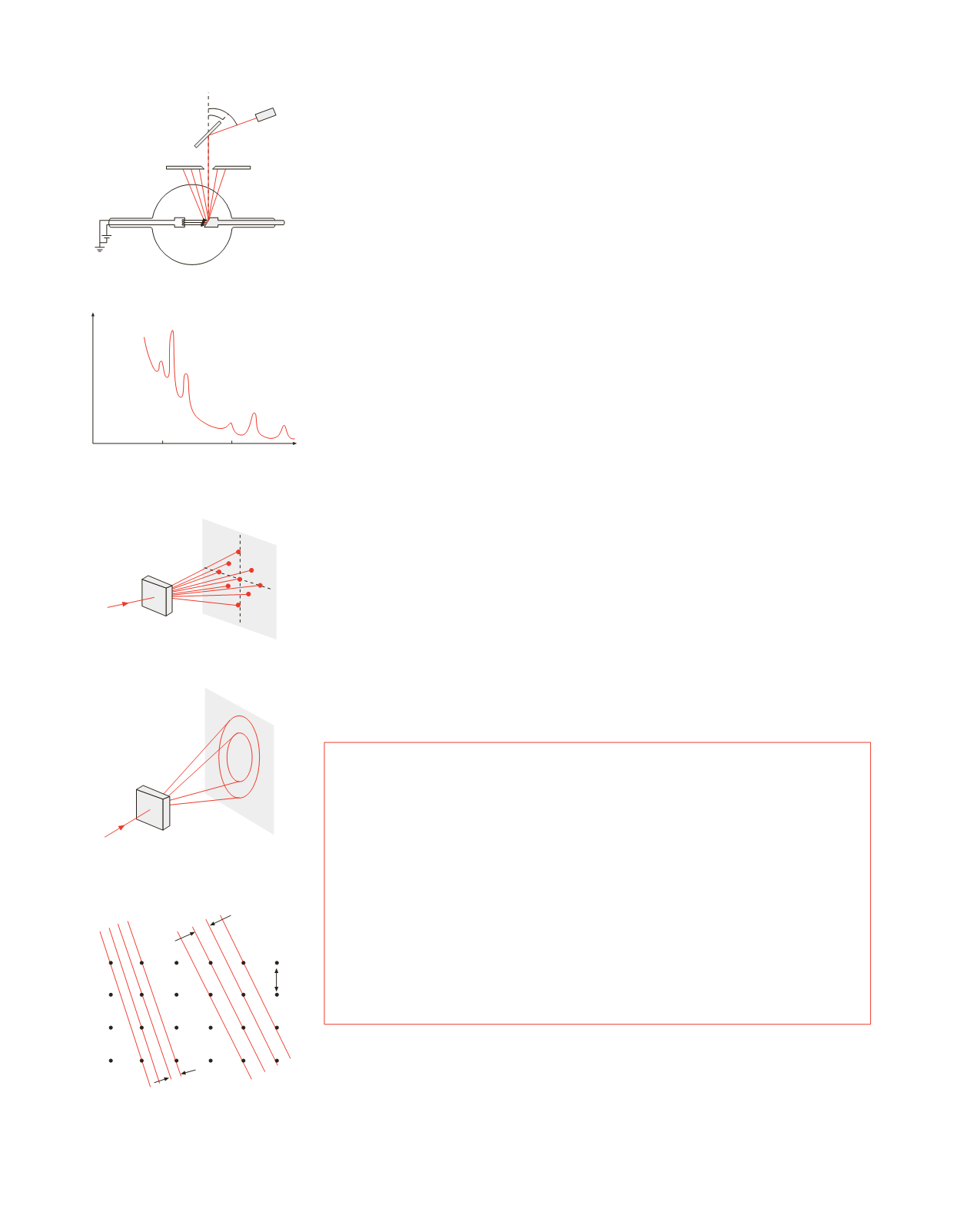
Esempio 16.14
Un fascio di raggi
X
di lunghezza d’onda
l
= 0.1 nm incide su un cristallo di NaCl che
funge da bersaglio nello spettrografo a cristallo. Calcolare gli angoli
q
ai quali si forma-
no i massimi di interferenza per i due sistemi di piani reticolari mostrati in figura.
Soluzione
Dalla figura si ricava, essendo
a
= 0.282 nm,
d
1
=
a
/ 5 = 0.126 nm ,
d
2
=
a
/ 10 = 0.089 nm .
I massimi si formano per
m
l
m
l
sen
q
= ––––– = 0.397
m
,
q
1
= 23.4°
q
2
= 52.7° , sen
q
= ––––– = 0.562
m
,
q
1
= 34.2°.
2
d
1
2
d
2
cristallo
fascio di
raggi
X
lastra
Figura 16.56
lastra
polvere
cristallina
Figura 16.57
Figura 16.58
d
1
d
2
a
X
















