
d
PR
1
ct
1
=
d
–
v
0
t
1
⇒
t
1
= –––––
c
+
v
0
d
PR
2
ct
2
=
d
+
v
0
t
2
⇒
t
2
= ––––– >
t
1
.
c
–
v
0
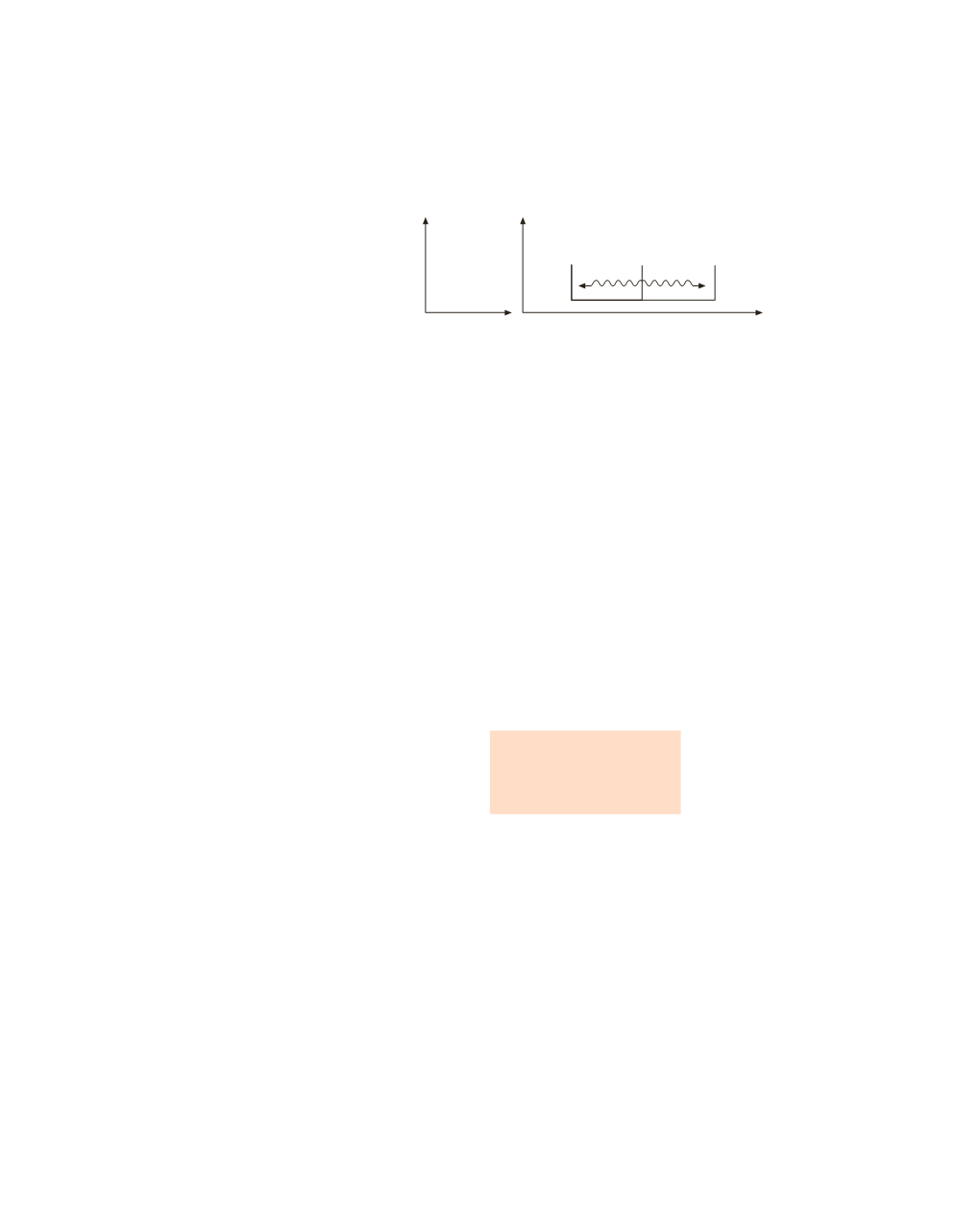
Nella visuale galileiana la velocità della luce si compone con la velocità di tra-
scinamento
v
0
: in
O
la luce che va da
P
a
R
1
ha velocità
c
–
v
0
e quella che va da
P
a
R
2
ha velocità
c
+
v
0
, per cui dobbiamo scrivere
PR
1
(
c
–
v
0
)
t
1
=
d
–
v
0
t
1
⇒
t
1
=
d/c
PR
2
(
c
+
v
0
)
t
2
=
d
+
v
0
t
2
⇒
t
2
=
d/c
e la simultaneità viene preservata; però questo procedimento è contrario al risultato
sperimentale dell’invarianza di
c
.
3.9 Quantità di moto ed energia relativistiche
La quantità di moto di un punto materiale di massa
m
e velocità
v
si scrive rela-
tivisticamente come
m
p
=
m
g
v
= ––––––––––
v
.
(3.19)
v
2
1 – –––
c
2
Non si ha più la dipendenza diretta dalla velocità della definizione newtoniana
m
v
ma compare anche
g
come fattore moltiplicativo. Si nota di nuovo che la definizio-
ne relativistica tende a quella newtoniana per piccole velocità.
La legge del moto si scrive nella forma (2.2)
d
p
F
= –––– ,
(3.20)
dt
cioè conserva formalmente la struttura newtoniana, purché la quantità di moto sia
data da (3.19). Ne vedremo più avanti l’applicazione in alcune situazioni che
abbiamo già trattato per piccole velocità. Vogliamo però notare subito come
l’applicazione di una forza, quando la velocità ha già assunto valori vicini a
c
, porta
sì ad un aumento di
p
, ma questo aumento non si traduce in un aumento corrispon-
dente di velocità, bensì soprattutto in un aumento del fattore
g
.
L’effetto si vede chiaramente mettendo in relazione la crescita di
p
con quella di
v
, nel modo seguente. Si differenzia la (3.19) e si divide per
p
=
m
g
v
:
118
Moti relativi
O
O
'
R
1
P
R
2
Figura 3.22
















