
(
r
',
v
',
a
' ) vanno riferite al sistema
O
e quindi è necessario stabilire le relazioni di trasforma-
zione che permettono di passare dalle coordinate valide in
O
' a quelle valide in
O
.
La semplicità della geometria della figura 3.2, scelta per il moto relativo traslatorio,
rende le formule di trasformazione praticamente immediate e di facile uso. In particolare, il
fatto che gli assi dei sistemi siano paralleli tra loro ha come conseguenza che le componenti
di un vettore siano le stesse nei due sistemi; ad esempio la componente
v
'
x
del vettore velocità
v
' è eguale alla componente
v
'
x
'
(si veda il paragrafo C.2 dell’appendice C). Se il sistema
O
'
avesse gli assi ruotati rispetto a quelli di
O
, con l’angolo tra assi omologhi costante durante il
moto, le formule di trasformazione sarebbero più complicate, pur restando le conclusioni
generali le stesse. Sempre con riferimento a
v
' e alla relazione
v
=
v
O
'
+
v
', nota la compo-
nente
v
'
x
'
si dovrebbe trasformarla in
v
'
x
e solo allora scrivere
v
x
=
v
O
',
x
+
v
'
x
, proiezione della
relazione vettoriale sull’asse
x
del sistema
O
.
Facciamo un esempio esplicito non per un moto relativo traslatorio, ma per il moto rota-
torio dei due sistemi del paragrafo 3.5: gli assi di
O
' ruotano a rispetto a quelli di
O
con velo-
cità angolare costante
w
e l’angolo tra
x
' e
x
è
q
=
w
t
: la (3.1) si riduce a
r
=
r
'. Ciò non vuol
dire che valgono le relazioni
x
=
x
',
y
=
y
', manifestamente false e concettualmente sbagliate
perché eguagliano le componenti viste da due diversi sistemi. Le relazioni corrette sono
r
x
=
r
'
x
,
r
y
=
r
'
y
, cioè
x
=
x
' cos
w
t
–
y
' sen
w
t
,
y
=
x
' sen
w
t
+
y
' cos
w
t
,
con il che l’eguaglianza è espressa nel sistema
O
, oppure passando nel sistema
O
'
r
x
'
=
r
'
x
'
,
r
y
'
=
r
'
y
'
, cioè
x
' =
x
cos
w
t
+
y
sen
w
t
,
y
' = –
x
sen
w
t
+
y
cos
w
t
.
Queste formule di trasformazione esprimono il legame tra le coordinate di uno stesso
punto nei due sistemi (ottenuti uno dall’altro tramite una rotazione nel piano
x
,
y
). Esse val-
gono anche per le componenti di un qualsiasi altro vettore. Notiamo esplicitamente, e lo si
verifica subito, che una rotazione lascia invariato il modulo di un vettore.
Si è già rivelato nella dimostrazione del teorema delle velocità relative (3.4) che
d
r
'/
dt
non è
v
'; analogamente
d
v
'/
dt
non è
a
'. Questo perché i versori
u
x
'
,
u
y
'
,
u
z
'
sono variabili nel
tempo, rispetto a
O
. L’osservatore
O
' trova però l’usuale cinematica: nel suo sistema
a
' =
d
v
'/
dt
e
v
' =
d
r
'/
dt
;
non gli torna invece che
a
=
d
v
/
dt
e
v
=
d
r
/
dt
.
La quarta relazione fondamentale, oltre alle tre citate sopra, è (3.10), che permette di
estendere la legge di Newton ai sistemi non inerziali. Questa però è l’unica estensione che ci
limitiamo a fare; cioè non cercheremo di sviluppare in un generico sistema lo studio della
dinamica del punto, come già fatto in un sistema inerziale partendo da (2.1). La procedura da
seguire piuttosto è di trasformare le misure eseguite in un sistema non inerziale riferendole a
un sistema inerziale e, a questo punto, interpretarle con le leggi note.
Anche tutti i successivi sviluppi della teoria (sistemi di punti e corpi rigidi) verranno
ambientati naturalmente in sistemi di riferimento inerziali, con una sola importante eccezio-
ne: troveremo significativo in qualche caso riferire il moto anche al cosiddetto sistema di
riferimento del centro di massa, che in generale non è un sistema inerziale. Avremo allora
modo di applicare il formalismo sviluppato in questo capitolo.
Nota sulla composizione di moti
Le operazioni essenzialmente formali di scomposizione del moto di un punto in tre moti
rettilinei lungo gli assi e viceversa, che abbiamo visto nel primo capitolo, trovano applica-
zione nell’ambito del moto relativo, anche se il contesto fisico è diverso. Il moto rispetto a
O
può sempre essere pensato come composizione del moto relativo rispetto a
O
' e del moto di
trascinamento di
O
' rispetto a
O
.
Commenti e note
107
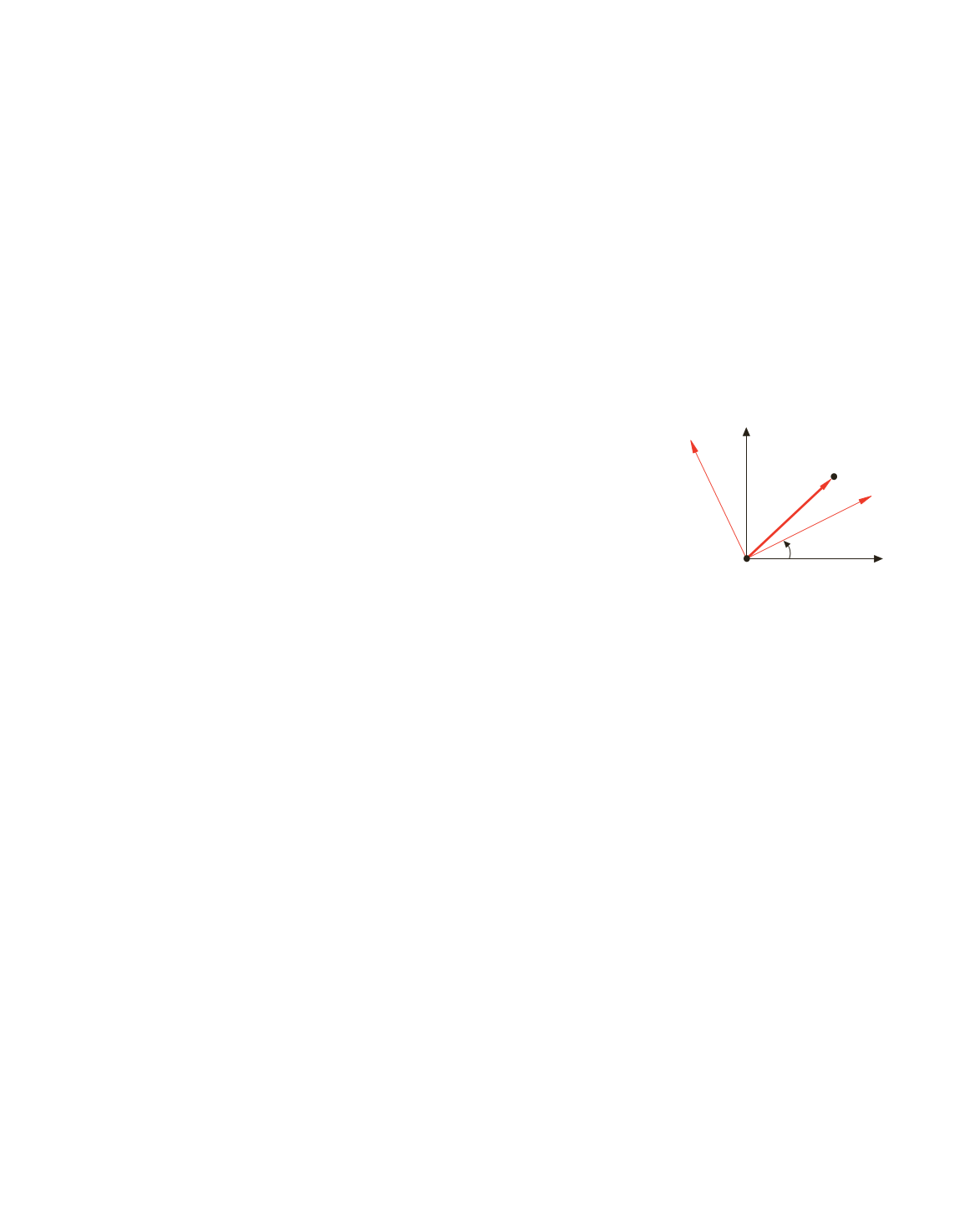
y
'
y
P
x
'
x
O O
'
q
=
w
t
r r
'
Figura 3.17
















