
g
=
g
0
–
w
×
(
w
×
R
) – 2
w
×
v
.
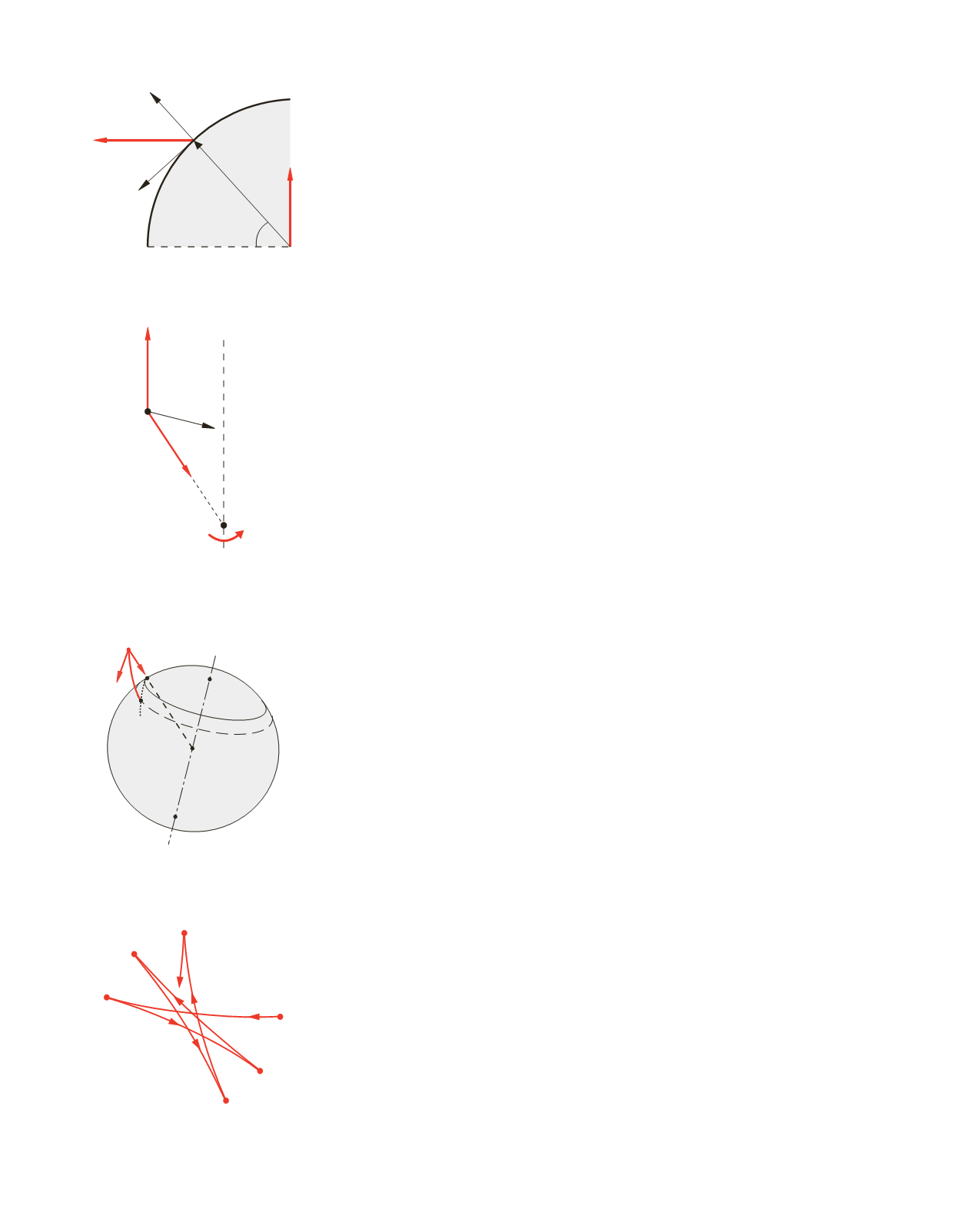
Il termine centrifugo è ortogonale all’asse
z
di rotazione e diretto verso l’esterno, in
entrambi gli emisferi. Esso vale in modulo, come già calcolato, 3.38 · 10
–2
cos
q
m/s
2
. Le due
componenti, radiale (parallela e concorde a
R
) e trasversa (diretta sempre verso l’equatore)
valgono rispettivamente
a
R
= 3.38 · 10
–2
cos
2
q
,
a
q
= 3.38 · 10
–2
cos
q
sen
q
m/s
2
.
La correzione centrifuga all’accelerazione di gravità è nulla al polo, dove
R
e
w
sono
paralleli, e massima all’equatore, dove sono ortogonali. Gli effetti sono la diminuzione (pic-
cola) del valore di
g
0
con dipendenza dalla latitudine
q
e l’alterazione della verticale determi-
nata con il filo a piombo; ad esempio per
q
= 45° la deviazione è dell’ordine di 0.1°.
L’effetto del termine di Coriolis è più complicato in quanto dipende dalla velocità
v
del
punto rispetto al sistema solidale con la terra.
Se per esempio consideriamo un punto che cade da un altezza
h
, con velocità iniziale
nulla, l’azione della forza centrifuga comporta uno spostamento verso l’equatore lungo un
meridiano; invece la forza di Coriolis, tangente a un parallelo e rivolta come in figura 3.14,
provoca uno spostamento verso
oriente
in entrambi gli emisferi. L’effetto complessivo è la
combinazione dei due.
Si trova che le due deviazioni rispetto al piede della verticale
vera
sono
x
centr
= 3.45 · 10
–3
h
cos
q
sen
q
m ,
x
Cor
= 2.2 · 10
–5
h
3/2
cos
q
m .
Con
h
= 100 m e
q
= 45° ,
x
centr
≅
17.3 cm ,
x
Cor
≅
1.6 cm .
Qual è la
spiegazione inerziale
degli effetti misurati? Il punto
P
che cade dall’altezza
h
(=
PQ
) ha velocità iniziale
v
P
, 0
, in quanto all’istante
t
= 0 sta ruotando insieme alla terra, e
accelerazione
g
0
. Il moto avviene nel piano individuato da
v
P
, 0
e
g
0
, la cui intersezione con
la superficie terrestre è indicata in figura 3.15 dalla linea punteggiata;
PP
rappresenta la
traiettoria del punto. La velocità iniziale è tangente a un parallelo, però durante la caduta non
c’è nessun vincolo che tenga il punto su una traiettoria circolare e perciò esso si sposta verso
l’equatore, come è chiaro dalla figura. Inoltre poiché
P
è inizialmente a una distanza
dall’asse di rotazione maggiore di quella di
Q
, esso ha velocità maggiore di
Q
e quindi cade
più a est di
Q
. Correttamente interpretati, questi effetti mettono in evidenza la rotazione ter-
restre.
Un effetto più vistoso a prova della rotazione terrestre è quello mostrato dal
pendolo di
Foucault
. Immaginiamo di fare oscillare un pendolo semplice al polo: il moto è contenuto
nel piano
g
0
,
v
, fisso in un sistema inerziale; però dalla terra, sistema non inerziale, si vede
ruotare il piano di oscillazione del pendolo, a causa della forza di Coriolis. Un giro completo
dura 24 ore. Se il pendolo lasciasse una traccia sul suolo si vedrebbero le linee disegnate in
figura 3.16. Naturalmente l’esperimento è stato eseguito alle nostre latitudini, ma l’effetto è
lo stesso anche se un giro completo viene compiuto in un tempo che dipende dalla latitudine.
È interessante osservare che i primati di lancio del giavellotto o del disco, a parità di con-
dizioni atmosferiche e di attrito dell’aria, sono influenzati in modo non trascurabile dalla
forza centrifuga e di Coriolis.
3.7 Commenti e note
Raccogliamo in questo paragrafo alcuni commenti e delle note che altrimenti avrebbero
appesantito il testo.
Una caratteristica importante di (3.1), (3.4), (3.7) è di essere relazioni vettoriali e quindi
valere intrinsecamente. Però ciascuna si può tradurre in tre relazioni tra le componenti dei
vari vettori in un determinato sistema di riferimento, che deve essere lo stesso per tutti i
termini. Se per esempio si sceglie il sistema
O
tutte le componenti dei termini con l’apice
106
Moti relativi
N
R
a
centr
q
w
Figura 3.13
w
v
– 2
w
×
v
Figura 3.14
P
N
Q
P
S
g
0
v
P, 0
Figura 3.15
Figura 3.16
















