
Moto di trascinamento rettilineo accelerato
101
la verticale la linea di caduta libera dei corpi, nel sistema
O
' c’è una verticale apparente
che forma l’angolo
q
con la verticale inerziale; un filo a piombo sul carrello si dispor-
rebbe ad angolo
q
rispetto all’asse
z
'. Dalla misura di
q
si può dedurre il valore di
a
t
e
determinare che il moto di trascinamento è accelerato; se fosse
a
t
= 0, sarebbe anche
q
= 0 e
d
= 0, il punto cadrebbe lungo l’asse
z
', come nella figura 3.6 dell’esempio 3.3.
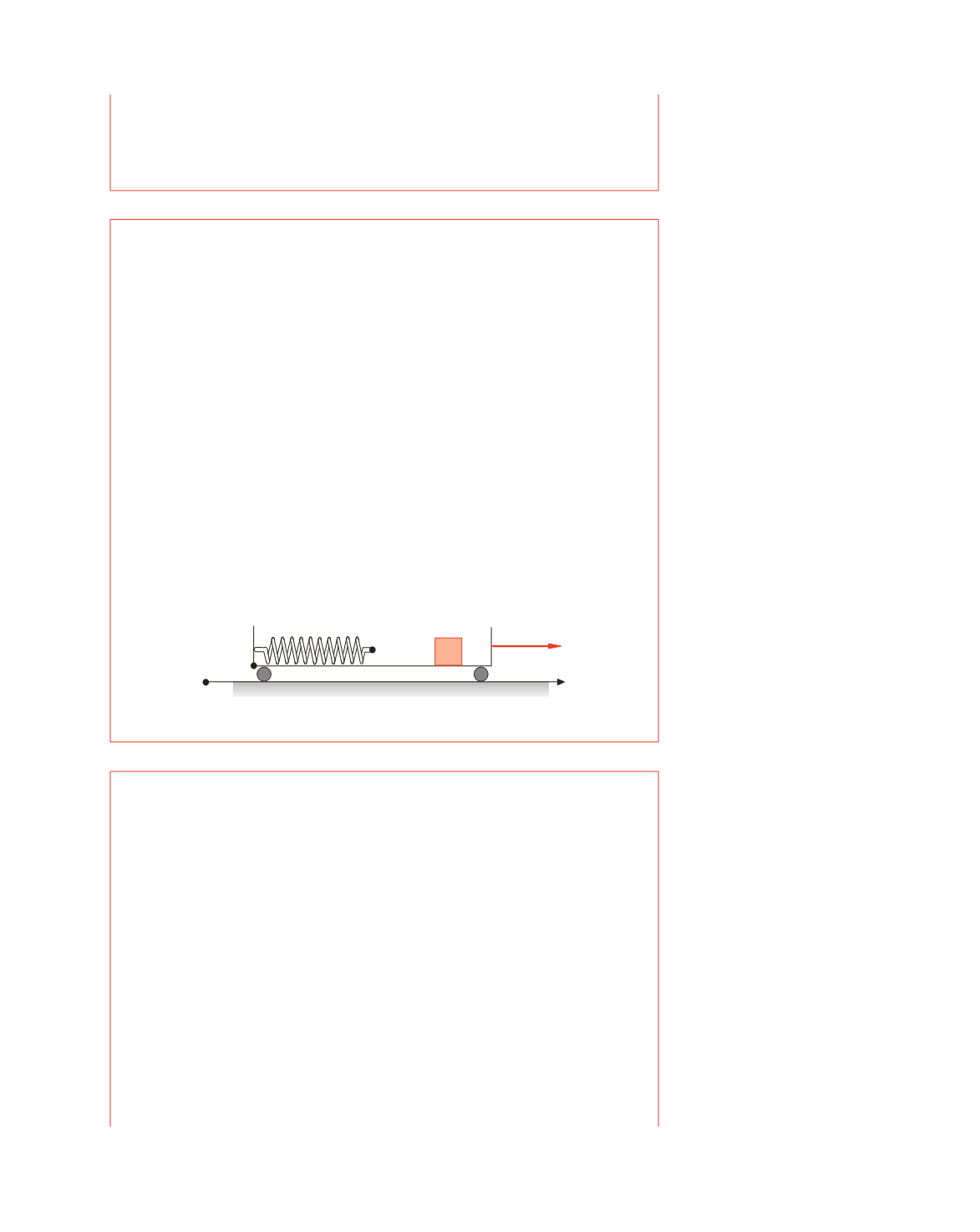
Esempio 3.5
Un punto materiale di massa
m
è posto sul pavimento liscio di un carrello che avanza con
accelerazione
a
t
rispetto al sistema inerziale
O
(figura 3.9). Ad un estremo del carrello è
fissata una molla di costante elastica
k
. Descrivere le osservazioni di
O
e
O
'.
Soluzione
Nel sistema inerziale si osserva la seguente successione di eventi. Il punto resta fermo
mentre il carrello gli scorre sotto (non c’è attrito) fino a quando l’estremo libero della
molla lo raggiunge. La molla inizia allora a comprimersi e il punto a muoversi; a regime
il punto è fermo rispetto al carrello e si muove con accelerazione
a
t
rispetto a
O
, la molla
è compressa della quantità
x
c
=
m
a
t
/k
: infatti è la forza elastica della molla che applica-
ta al punto gli comunica l’accelerazione
a
t
(
kx
c
=
m
a
t
).
Per l’osservatore
O
', solidale al carrello, inizialmente il punto è in moto con accelerazio-
ne –
a
t
(in effetti
a
' =
a
–
a
t
= –
a
t
dato che
a
= 0). Ad un certo istante il punto raggiunge
la molla che inizia a comprimersi e alla fine il punto è fermo, con la molla compressa
della quantità
x
c
.
O
' conclude che sul punto, apparentemente libero, agisce invece la
forza –
m
a
t
che viene bilanciata, raggiunto l’equilibrio statico, dalla forza elastica della
molla:
kx
c
=
m
a
t
.
Notiamo che dalla misura di
x
c
si può dedurre il valore di
a
t
. La molla di questo esem-
pio, come il filo a piombo del precedente, costituisce in sostanza un
accelerometro
, che
misura l’accelerazione del sistema non inerziale.
k
m
O
'
O
x
a
t
Figura 3.9
Esempio 3.6
Un sistema con origine
O
' e asse
z
' verticale è solidale ad un ascensore che si muove
lungo l’asse
z z
' di un sistema inerziale con origine in
O
. L’ascensore inizia a salire
con accelerazione
a
t
, parallela e concorde all’asse
z
', descrive poi un moto uniforme e
infine decelera con accelerazione –
a
t
fino a fermarsi. Se nell’ascensore si compiono
esperimenti di caduta libera dei corpi, che accelerazioni
a
' si misurano nelle tre fasi del
moto?
Soluzione
Nel sistema inerziale
a
=
g
e quindi la relazione tra le accelerazioni è
g
=
a
' +
a
t
⇒
a
' =
g
–
a
t
.
Proiettando sull’asse
z
' abbiamo:
a
t
> 0
a
' = –
g
–
a
t
= – (
g
+
a
t
) ,
a
t
= 0
a
' = –
g
,
a
t
< 0
a
' = –
g
– (–
a
t
) = – (
g
–
a
t
) .
















