
Infine per le accelerazioni è
a
' =
a
, dato che ambedue i sistemi sono inerziali.
Le relazioni (3.11), che permettono di calcolare le coordinate del punto in un
sistema inerziale note quelle nell’altro sistema inerziale, esprimono una
trasforma-
zione galileiana
tra i due sistemi; analogamente (3.12) è la trasformazione galileia-
na delle velocità.
Negli esempi seguenti esaminiamo alcuni casi particolari di moto del punto
P
. La figura di riferimento per il moto relativo dei due sistemi è sempre la 3.2, con
v
O
'
costante.
Moto di trascinamento rettilineo uniforme
97
Esempio 3.1
Un punto
P
descrive nel piano
x
,
y
un moto rettilineo uniforme con velocità
v
, di com-
ponenti
v
x
e
v
y
, partendo all’istante
t
= 0 dalla posizione di coordinate
x
0
,
y
0
. Determinare
il moto visto dal sistema
O
'.
Soluzione
Scriviamo le equazioni dei moti proiettati sugli assi servendoci di (3.11):
x
=
x
0
+
v
x
t
,
x
' =
x
–
v
O
'
t
=
x
0
+ (
v
x
–
v
O
'
)
t
,
y
=
y
0
+
v
y
t
,
y
' =
y
=
y
0
+
v
y
t
,
z
= 0
,
z
' =
z
= 0 .
Anche nel sistema
O
' le componenti della velocità del punto sono costanti e quindi il
moto è rettilineo uniforme (come ci aspettiamo essendo i due sistemi inerziali: se
a
= 0 anche
a
' = 0). Però l’inclinazione della traiettoria rispetto all’asse
x x
' è diversa
nei due sistemi, così come è diverso il modulo della velocità:
v
y
v
'
y
v
y
tg
f
= ––– , tg
f
' = ––– = –––––––– ,
v
x
v
'
x
v
'
x
–
v
O
'
v
=
v
x
2
+
v
y
2
,
v
' = (
v
x
–
v
O
'
)
2
+
v
y
2
.
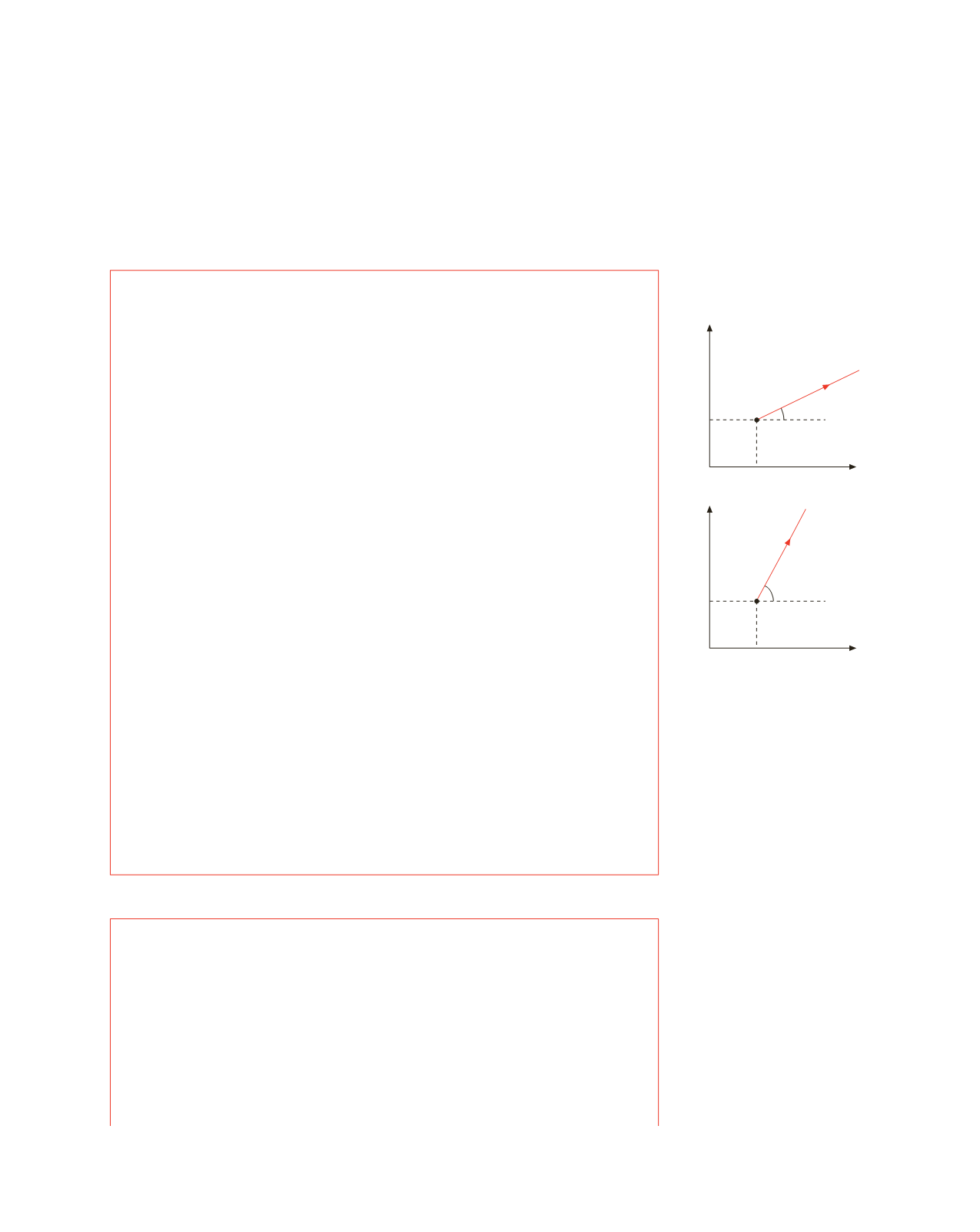
Nella figura 3.3 è mostrato un caso particolare in cui
v
O
'
è positiva e minore di
v
x
(si
ricordi che nell’istante iniziale le origini dei due sistemi coincidono).
Se fosse
v
O
'
=
v
x
, cioè se il sistema
O
' si muovesse con velocità eguale alla componen-
te
v
x
della velocità del punto, sarebbe
v
x
' = 0 e il moto visto da
O
' risulterebbe parallelo
all’asse
y y
'. Solo quando il moto in
O
è parallelo all’asse
x
, cioè all’asse della trasla-
zione tra i due sistemi, anche in
O
' si osserva un moto parallelo all’asse
x
'.
Riassumendo, entrambi gli osservatori vedono un moto rettilineo uniforme e concorda-
no sul fatto che l’accelerazione è nulla e che quindi non ci sono forze agenti; le traietto-
rie appaiono diverse, e percorse con velocità diverse, perché nei due sistemi sono diver-
se le condizioni iniziali (
v
x
≠
v
'
x
).
y
y
0
x
0
x
f
O
y
'
y
0
x
0
x
'
f
'
O
'
Figura 3.3 (Esempio 3.1)
Esempio 3.2
Un punto
P
compie nel piano
x, y
un moto rettilineo uniformemente accelerato con acce-
lerazione
a
, di componenti
a
x
e
a
y
, partendo con velocità iniziale nulla dall’origine.
Determinare il moto visto nel sistema
O
'.
Soluzione
Ricorriamo di nuovo a (3.11) e anche a (3.12):
1
1
x
= ––
a
x
t
2
,
x
' =
x
–
v
O
'
t
= ––
a
x
t
2
–
v
O
'
t
,
2
2
















