
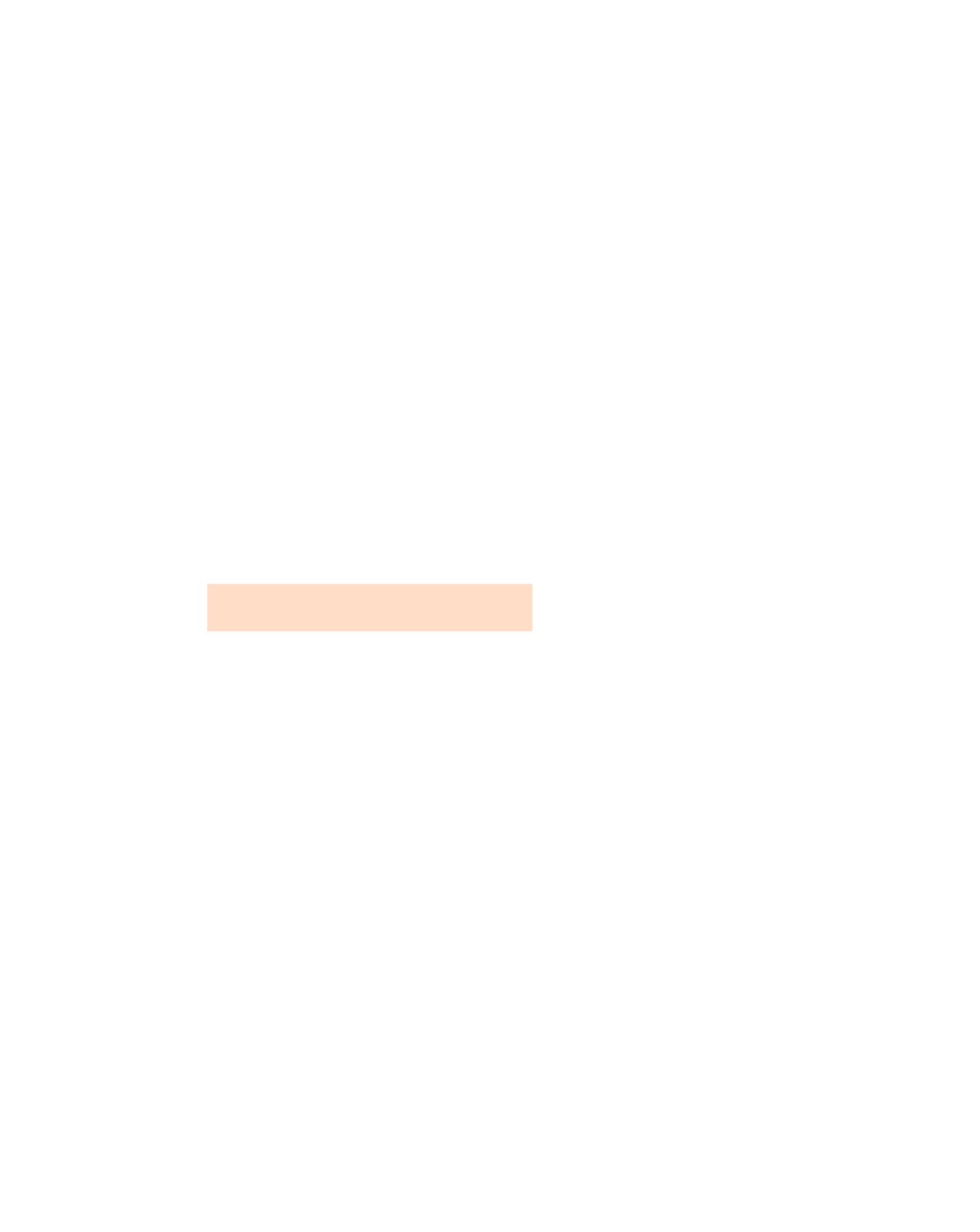
mentre rispetto al sistema mobile l’
accelerazione relativa
è
d
2
x
'
d
2
y
'
d
2
z
'
a
' = ––––
u
x
'
+ ––––
u
y
'
+ ––––
u
z
'
.
dt
2
dt
2
dt
2
L’accelerazione dell’origine del sistema mobile
O
' rispetto a
O
è data da
a
O
'
=
d
v
O
'
/
dt
. Derivando (3.4) rispetto al tempo otteniamo:
d
v
d
v
O
'
d
v
'
d
w
d
r
'
a
= ––– = –––– + ––– + ––––
×
r
' +
w
×
––– .
dt
dt
dt dt
dt
Calcoliamo
d
v
'/
dt
:
d
v
'
d dx
'
dy
'
dz
'
d
2
x
'
d
2
y
'
––– = –––
(
–––
u
x
'
+ –––
u
y
'
+ –––
u
z'
)
= ––––
u
x
'
+ ––––
u
y
'
+
dt dt dt dt dt
dt
2
dt
2
d
2
z
'
dx
'
d
u
x'
dy
'
d
u
y'
dz
'
d
u
z'
+ ––––
u
z
'
+ –––– –––– + –––– –––– + ––– –––– =
a
' +
w
×
v
' .
dt
2
dt dt dt dt dt dt
Abbiamo di nuovo utilizzato le formule di Poisson per il calcolo delle derivate dei
vettori degli assi mobili. Da (3.5) si ha inoltre
d
r
'
w
×
––– =
w
×
v
' +
w
×
(
w
×
r
')
dt
e pertanto
d
w
a
=
a
' +
a
O
'
+
w
×
(
w
×
r
') + –––
×
r
' + 2
w
×
v
' .
(3.7)
dt
Le accelerazioni del punto
P
misurate nei due sistemi non coincidono, ma sono
messe in relazione tramite la (3.7), detta
teorema delle accelerazioni relative
.
Per valutare l’
accelerazione di trascinamento
a
t
riprendiamo la discussione
fatta per la velocità di trascinamento. L’accelerazione di trascinamento è quella del
punto
P
*
,
solidale col sistema mobile, che coincide nell’istante considerato col
punto
P
. Per
P
*
a
' e
v
' sono nulle e da (3.7)
d
w
a
t
=
a
O
'
+
w
×
(
w
×
r
') + –––
×
r
' .
(3.8)
dt
Possiamo pertanto riscrivere (3.7) come
a
=
a
' +
a
t
+
a
c
;
l’ultimo termine
a
c
= 2
w
×
v
'
(3.9)
è chiamato
accelerazione complementare o di Coriolis
; esso dipende dal moto di
P
rispetto al sistema mobile tramite la velocità relativa
v
'.
La complessa struttura della (3.7) fa comprendere quanto possa essere diversa
la descrizione del moto di uno stesso punto visto da due sistemi diversi.
Conseguentemente saranno diverse le forze che vengono
ipotizzate
per spiegare il
determinato tipo di moto da parte degli osservatori solidali a differenti sistemi di
riferimento. Passeremo quindi ad esaminare, dopo le relazioni cinematiche, gli
aspetti dinamici del moto relativo. Prima trattiamo però un particolare caso cine-
matico di moto relativo.
Sistemi di riferimento. Velocità e accelerazione relative
93
Teorema delle accelerazioni
relative
Accelerazione di trascinamento
Accelerazione di Coriolis
















