
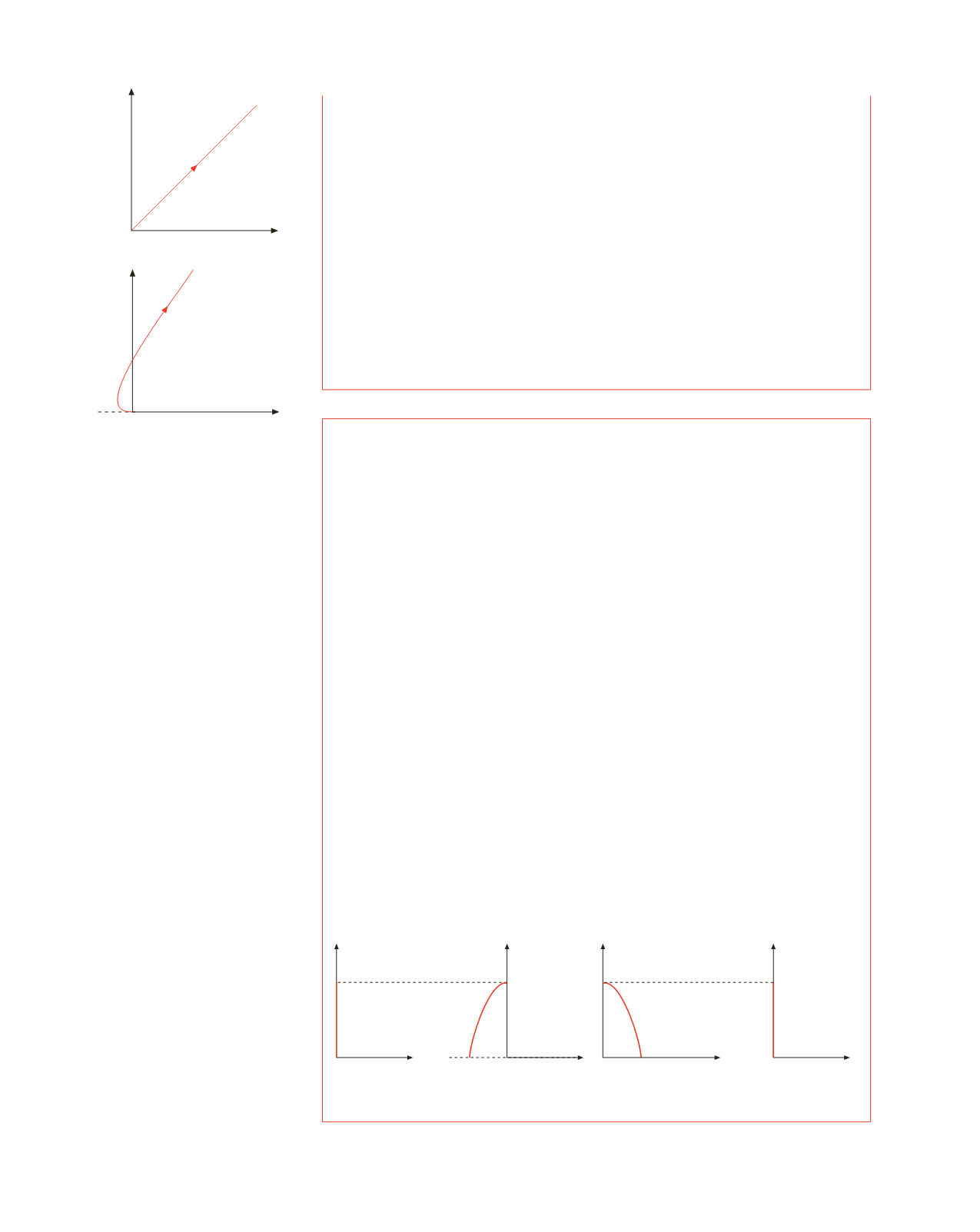
98
Moti relativi
1
1
y
= ––
a
y
t
2
,
y
' =
y
= ––
a
y
t
2
,
2
2
v
x
=
a
x
t
,
v
'
x
=
v
x
–
v
O
'
=
a
x
t
–
v
O
'
,
v
y
=
a
y
t
,
v
'
y
=
v
y
=
a
y
t
.
O
vede una traiettoria rettilinea con pendenza
v
y
/
v
x
=
a
y
/
a
x
. Invece
O
' vede una traiet-
toria curva: infatti la pendenza
v
'
y
a
y
t
––– = –––––––––
v
'
x
a
x
t
–
v
O
'
dipende dal tempo; la velocità iniziale è negativa, pari a –
v
O
'
. In figura 3.4 è mostrato
un caso particolare.
Per entrambi gli osservatori l’accelerazione è la stessa e quindi la forza è la stessa, paral-
lela e concorde alla traiettoria vista da
O
;
O
' vede una traiettoria curva in quanto la forza
e la velocità iniziale non sono parallele. Solo se
a
y
= 0, cioè se in
O
la traiettoria coinci-
de con l’asse
x
, anche
O
' vede un moto rettilineo uniformemente accelerato.
y
x
y
'
x
'
O
O
'
Figura 3.4 (Esempio 3.2)
Esempio 3.3
Nel sistema
O
un punto viene lasciato cadere lungo l’asse
z
, da un’altezza
h
. Cosa vede
O
'?
Soluzione
Le equazioni del moto nel sistema
O
sono:
1
x
= 0 ,
y
= 0 ,
z
=
h
– ––
gt
2
,
2
v
x
= 0 ,
v
y
= 0 ,
v
z
= –
gt
.
Invece in
O
' abbiamo:
1
x
' = –
v
O
'
t
,
y
' = 0 ,
z
' =
h
– ––
gt
2
,
2
v
'
x
= –
v
O
'
,
v
'
y
= 0 ,
v
'
z
= –
gt
.
Quindi in
O
' il moto è composto da un moto rettilineo uniforme lungo l’asse
x
' con velo-
cità –
v
O
'
e da un moto uniformemente accelerato lungo l’asse
z
: la traiettoria è un arco
di parabola, e si verifica facilmente che il punto cade a distanza –
v
O
'
2
h/g
dall’origine
O
'. Come nell’esempio 3.2, entrambi gli osservatori misurano la stessa accelerazione,
ma vedono traiettorie diverse perché sono diverse le condizioni iniziali.
Se invece il punto inizialmente è in quiete rispetto ad
O
' (e si muove quindi con velocità
v
O
'
rispetto ad
O
), durante la caduta esso continua a muoversi orizzontalmente con la stes-
sa velocità di
O
' e pertanto in
O
' cade verticalmente. Per
O
il punto ha la velocità iniziale
v
O
'
e cadendo descrive un arco di parabola, con uno spostamento dall’origine eguale a
quello prima calcolato (figure 3.5 e 3.6).
La caduta appare verticale nel sistema in cui il punto è in quiete e appare parabolica
nell’altro sistema. Dalla forma della traiettoria l’osservatore non può dedurre se è in
quiete o in moto rettilineo uniforme.
Figura 3.6
Figura 3.5
z
z
z
'
h
x
x
'
z
'
x
x
'
















