
104
Moti relativi
A conclusione della serie di esempi di questo paragrafo e dei precedenti, voglia-
mo brevemente riprendere l’argomento delle forze d’inerzia. Da una parte dobbia-
mo ripetere che esse non hanno esistenza reale in quanto non derivano dalle intera-
zioni fondamentali e non compaiono nella descrizione del moto effettuata in un
sistema di riferimento inerziale. Per altro in un sistema non inerziale esse rappre-
sentano effetti genuini e sono necessarie per spiegare le osservazioni sperimentali.
Ad esempio, in un sistema rotante è corretto attribuire alla forza centrifuga la ten-
denza allo spostamento radiale verso l’esterno e alla forza di Coriolis l’incurva-
mento della traiettoria osservata, in un veicolo che accelera o rallenta lo sposta-
mento all’indietro o in avanti è reale e si spiega solo con la forza –
m
a
t
. La cosa
importante è avere ben chiara l’origine di tali forze apparenti, utilizzarle corretta-
mente dove appropriato e non estendere la loro esistenza ai sistemi inerziali.
3.6 Il moto rispetto alla terra
Nei paragrafi precedenti abbiamo introdotto la nozione di sistema inerziale
senza però darne un esempio: lo facciamo adesso, dicendo che un sistema di riferi-
mento con l’origine nel centro di massa del sistema solare e gli assi diretti verso
determinate
stelle fisse
è con ottima approssimazione un sistema inerziale, come lo
sono tutti gli altri sistemi in moto rettilineo uniforme rispetto ad esso. La verifica è
data dal fatto che, entro gli errori sperimentali, in tali sistemi vale la legge di
Newton (2.1) con tutte le sue conseguenze; in particolare risultano accuratissime le
previsioni sul moto dei vari corpi celesti e dei satelliti artificiali.
Di norma le misure vengono fatte in un riferimento terrestre: ora, qualsiasi rife-
rimento solidale alla terra, per esempio con un asse diretto come l’asse terrestre e
gli altri due nel piano dell’equatore, ruota insieme alla terra e non è inerziale; anche
un sistema con origine nel centro della terra e assi sempre paralleli a quelli dei siste-
mi inerziali di cui sopra non è inerziale in quanto si muove di moto traslatorio acce-
lerato (la traiettoria dell’origine è curvilinea). Quindi nelle misure terrestri com-
y
'
y
y
'
y
'
y
'
y
y
y
y
y
'
x
'
x
x
x
x
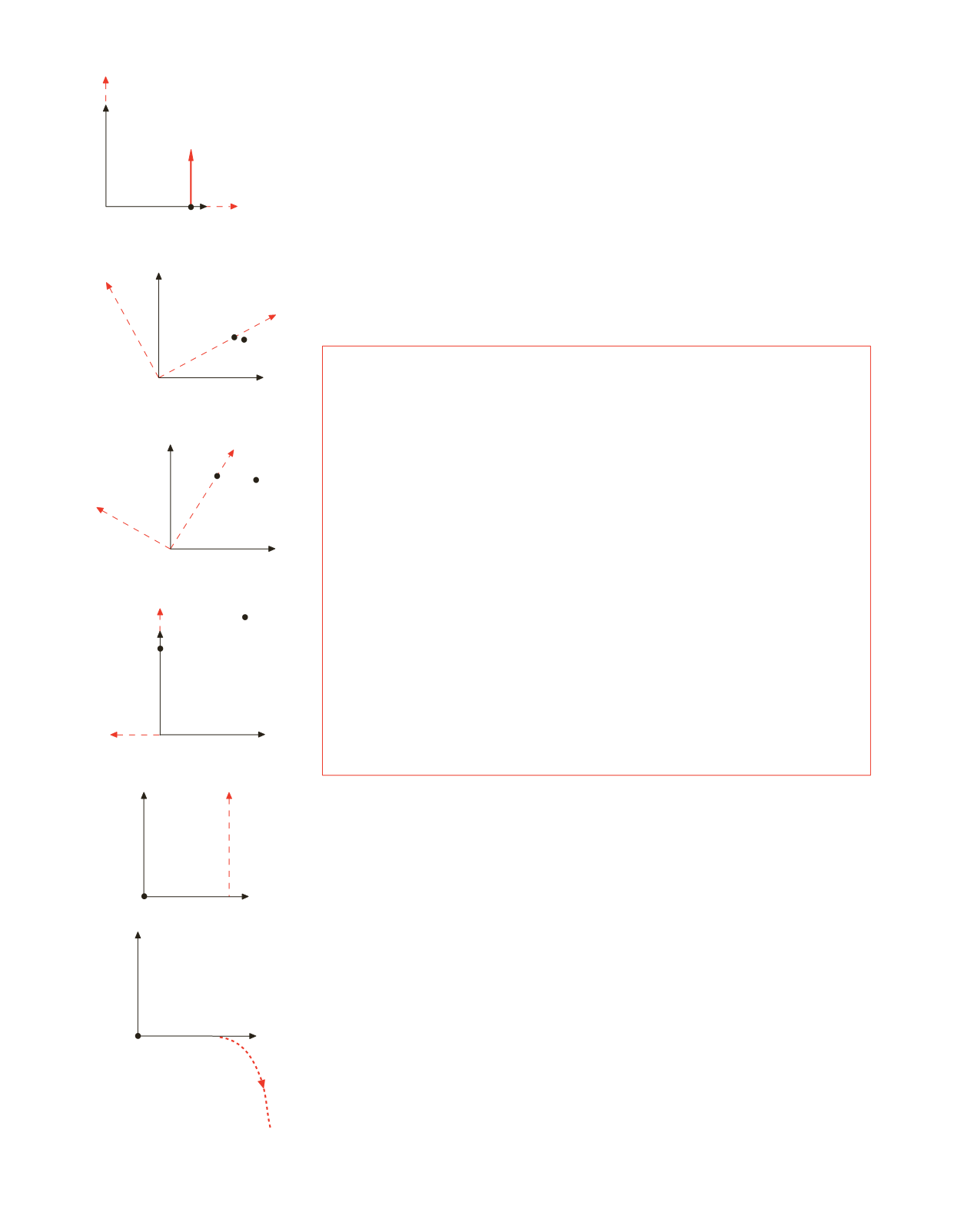
traiettoria
vista da
O
traiettoria
vista da
O
'
x
'
x
'
x
'
P
P
P
P
*
P
*
P
*
x
x'
P
*
P
t
= 0
t
=
T
/12
t
=
T
/6
t
=
T
/4
Figura 3.11
Esempio 3.7
Un cilindro cavo, di raggio
R
= 2 m, ruota rispetto al proprio asse verticale con velocità
angolare
w
. Un corpo poggiato contro la parete interna del cilindro ruota insieme ad
esso, ma non cade. Se il coefficiente di attrito statico tra corpo e parete del cilindro è
m
s
= 0.7, calcolare il valore minimo che deve avere
w
.
Soluzione
Risolviamo prima il problema in un sistema inerziale fisso al suolo (si veda l’esempio
2.10). La reazione
N
della parete, dovuta al fatto che il corpo tendendo a proseguire in
linea retta preme sulla parete, è la forza centripeta che permette la rotazione del corpo,
N
=
m
w
2
R
. Dato che il corpo non cade deve essere
mg
≤
m
s
N
=
m
s
m
w
2
R
g
⇒
w
2
≥
–––– ,
w
≥
2.6 rad/s.
m
s
R
Nel sistema rotante solidale al cilindro il corpo è in equilibrio statico, sia orizzontale che
verticale. Orizzontalmente esso è sottoposto alla reazione
N
e alla forza centrifuga
m
w
2
R
, che devono essere eguali in modulo (e sono opposte in verso); verticalmente la
condizione è quella già scritta nel sistema inerziale (non c’è accelerazione di trascina-
mento verticale). Si trova ovviamente lo stesso risultato, ma bisogna introdurre la forza
centrifuga, che non esiste nel sistema inerziale.
















