
paiono termini correttivi dovuti alle forze apparenti ed è conveniente riferire tali
misure, attraverso note formule di trasformazione, a un sistema inerziale (si sa, per
esempio, che il moto dei pianeti visto dalla terra è molto complicato). Le correzioni
hanno un’importanza che è in relazione con le misure e con la precisione voluta:
nel caso di misure astronomiche sono fondamentali, come pure nei moti terrestri su
notevoli distanze; per tempi e percorsi brevi possono essere trascurabili in assoluto
o rispetto ad altri effetti più importanti, come l’attrito dell’aria.
Dato che intendiamo descrivere e valutare quantitativamente gli effetti dovuti al moto
della terra, cominciamo col fornire alcuni dati numerici. Approssimiamo la terra ad una sfera
che compie un moto di rivoluzione attorno al sole lungo un’orbita ellittica, che praticamente
coincide con una circonferenza, ed un moto di rotazione su se stessa. I dati caratteristici delle
proprietà fisiche della terra e dei due moti, rivoluzione e rotazione, sono riportati nella tabel-
la che segue.
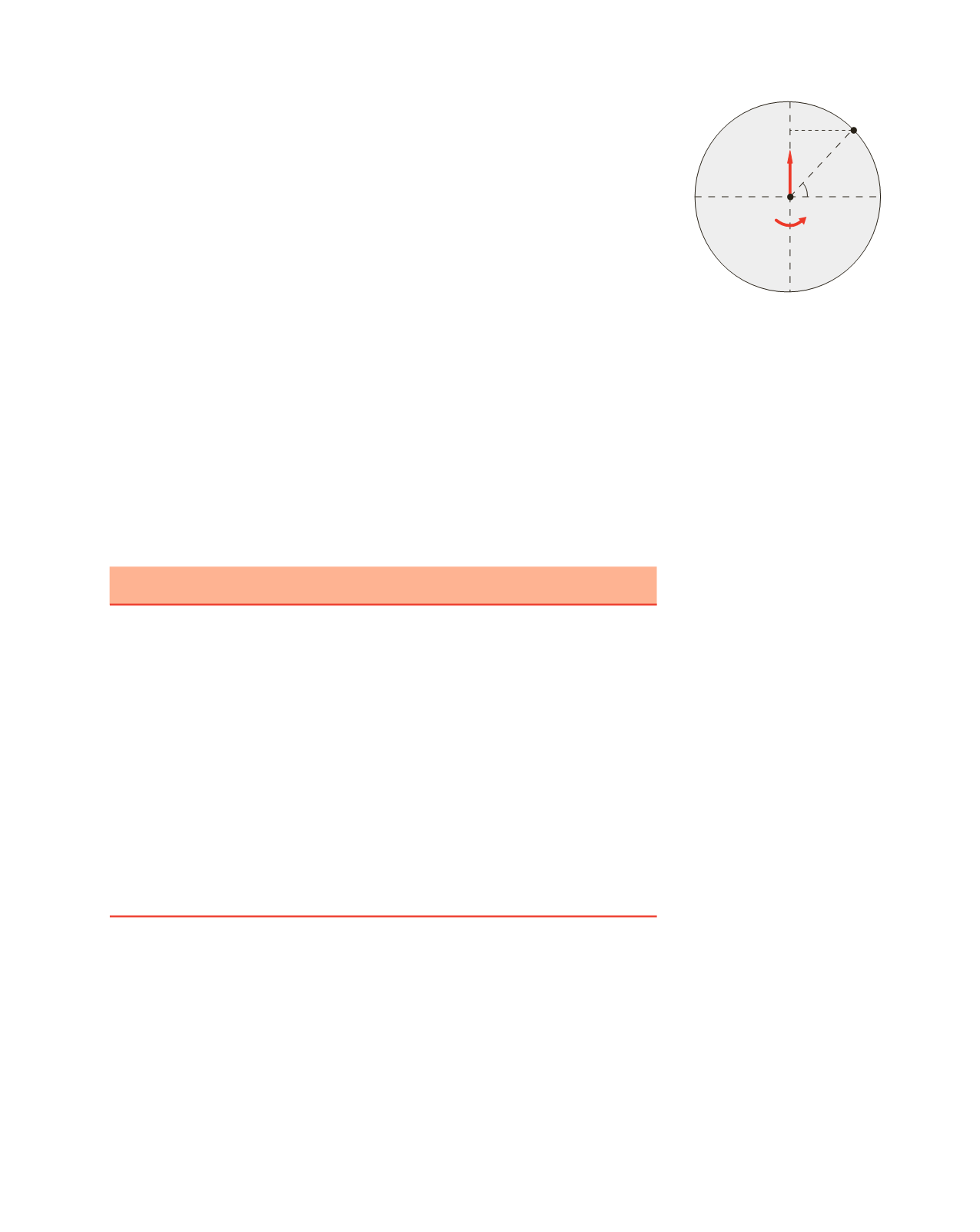
La velocità e l’accelerazione di un punto
P
alla superficie della terra (si veda figura 3.12)
sono
v
(
P
) =
w
r
=
w
R
cos
q
= 4.64 · 10
2
cos
q
m/s ,
a
(
P
) =
w
2
r
=
w
2
R
cos
q
= 3.38 · 10
–2
cos
q
m/s
2
.
In particolare, per un punto all’equatore
v
= 4.64 · 10
2
m/s = 1671 km / h ,
a
= 3.38 · 10
–2
m/s
2
.
Un sistema di riferimento solidale alla terra, con asse
z
orientato da sud a nord e assi
x
,
y
nel piano equatoriale, ruota con velocità angolare
w
=
w
u
z
, essendo
u
z
il versore dell’asse
z
e
w
= 7.29 · 10
–5
rad/s.
Un punto in moto vicino alla superficie terrestre è sottoposto alla forza peso
m
g
0
e in
base a (3.7)
g
0
=
g
+
w
×
(
w
×
R
) + 2
w
×
v
dove
g
e
v
sono rispettivamente l’accelerazione e la velocità misurate nel sistema solidale alla
terra. Abbiamo trascurato l’accelerazione centripeta del centro della terra, dovuta al moto di
rivoluzione. Pertanto l’accelerazione di gravità misurata dal sistema terrestre è data da
Il moto rispetto alla terra
105
N
P
r
R
q
S
w
Figura 3.12
massa della terra
m
T
5.98 · 10
24
kg
raggio della terra
R
6.37 · 10
6
m
raggio dell’orbita
R
0
1.49 · 10
11
m
periodo di rivoluzione
T
0
3.16 · 10
7
s
2
p
R
0
velocità di rivoluzione
v
0
= ––––– 2.96 · 10
4
m/s = 106655 km/h
T
0
2
p
velocità angolare di rivoluzione
w
0
= –––
1.99 · 10
–7
rad/s
T
0
accelerazione centripeta di rivoluzione
a
0
=
w
2
0
R
0
5.88 · 10
–3
m/s
2
periodo di rotazione
T
8.64 · 10
4
s
2
p
velocità angolare di rotazione
w
= –––
7.29 · 10
–5
rad/s
T
Tabella 3.1 Dati sul moto della terra
















