
Moti relativi
3.1 Sistemi di riferimento. Velocità e accelerazione relative
Sperimentalmente è provato con estrema accuratezza che
le leggi fisiche non
dipendono dalla scelta del sistema di riferimento
. Fissato un sistema di riferimento e
stabilita una certa proprietà, questa resta vera anche se cambiano l’origine e l’orienta-
zione degli assi coordinati, ovvero se ci riferiamo ad un altro sistema ottenuto dal
primo con una traslazione (spostamento dell’origine, conservando la stessa direzione
degli assi) o con una rotazione (stessa origine, cambio della direzione degli assi) o
con una operazione combinata. Non esiste pertanto un punto privilegiato dello spazio
e nemmeno un’orientazione privilegiata:
lo spazio appare omogeneo e isotropo
.
La caratteristica sostanziale di invarianza acquista un aspetto formale se le
leggi fisiche vengono espresse come relazioni tra entità che godono anch’esse delle
suddette proprietà di invarianza, come le grandezze scalari o quelle vettoriali o
altre più complesse, come ad esempio i tensori.
La situazione si presenta diversa quando un fenomeno viene osservato da due
sistemi di riferimento in moto l’uno rispetto all’altro. Nel caso del moto di un corpo
abbiamo già rilevato come il concetto stesso di moto sia relativo; un esempio sem-
plice è quello di una persona seduta in un mezzo di trasporto in movimento: essa è
in quiete rispetto al mezzo, ma è in movimento rispetto al suolo con la velocità che
ha il mezzo. Più in generale, il moto viene descritto con leggi diverse in due sistemi
di riferimento in moto relativo, a meno che questo moto non abbia certe caratteristi-
che che tra breve specificheremo. Non sussiste cioè invarianza delle leggi fisiche
rispetto a due sistemi di riferimento in moto qualsiasi l’uno rispetto all’altro.
Teorema delle velocità relative
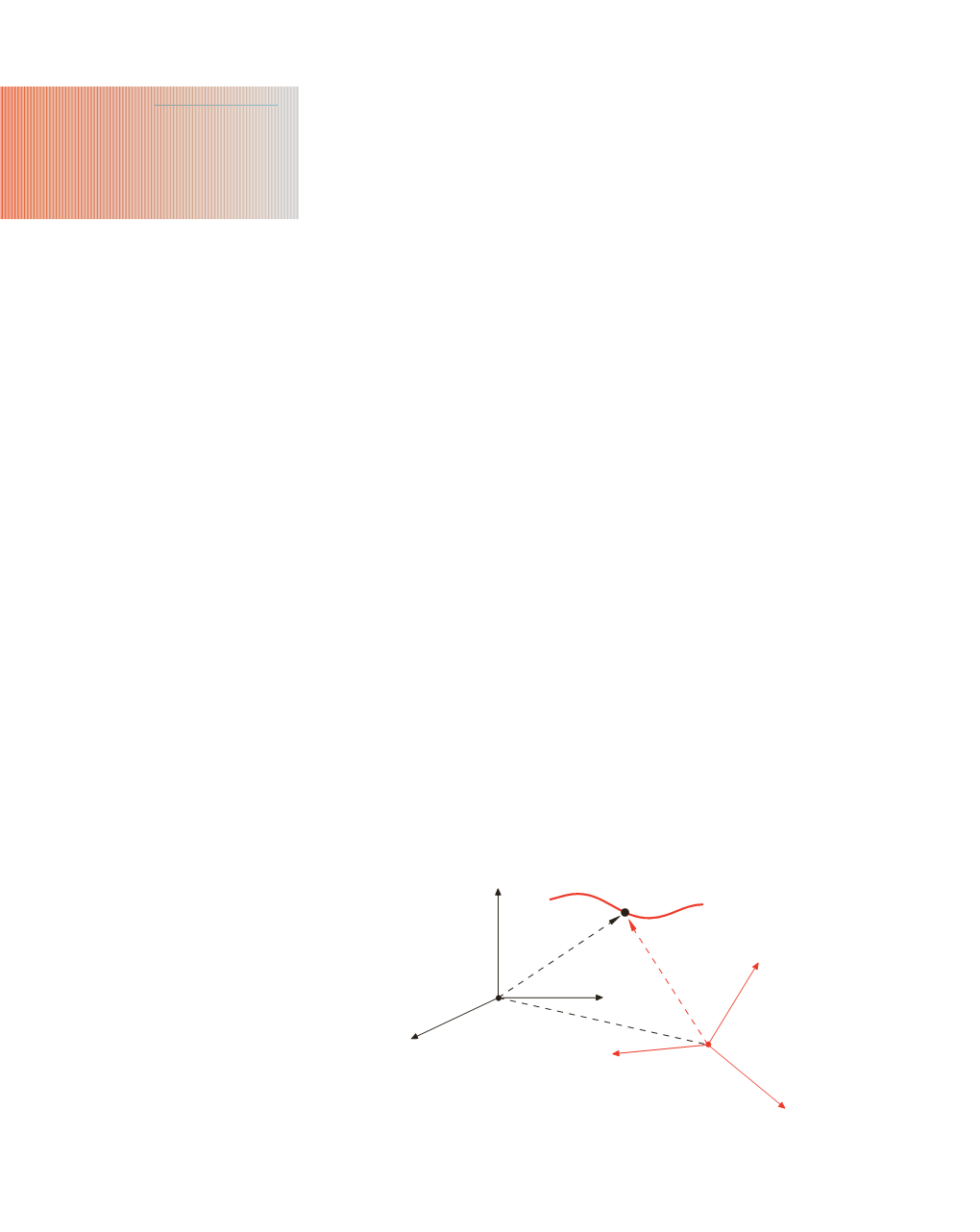
Nella figura 3.1 è rappresentato un punto
P
in movimento lungo una generica
traiettoria. Il suo moto viene osservato da una terna cartesiana con centro in
O
che,
Figura 3.1
z
P
z
'
y
'
y
x
x
'
O
'
O
r
r
'
3
















