
186
Parte Terza
I test attitudinali
www.
edises
.it
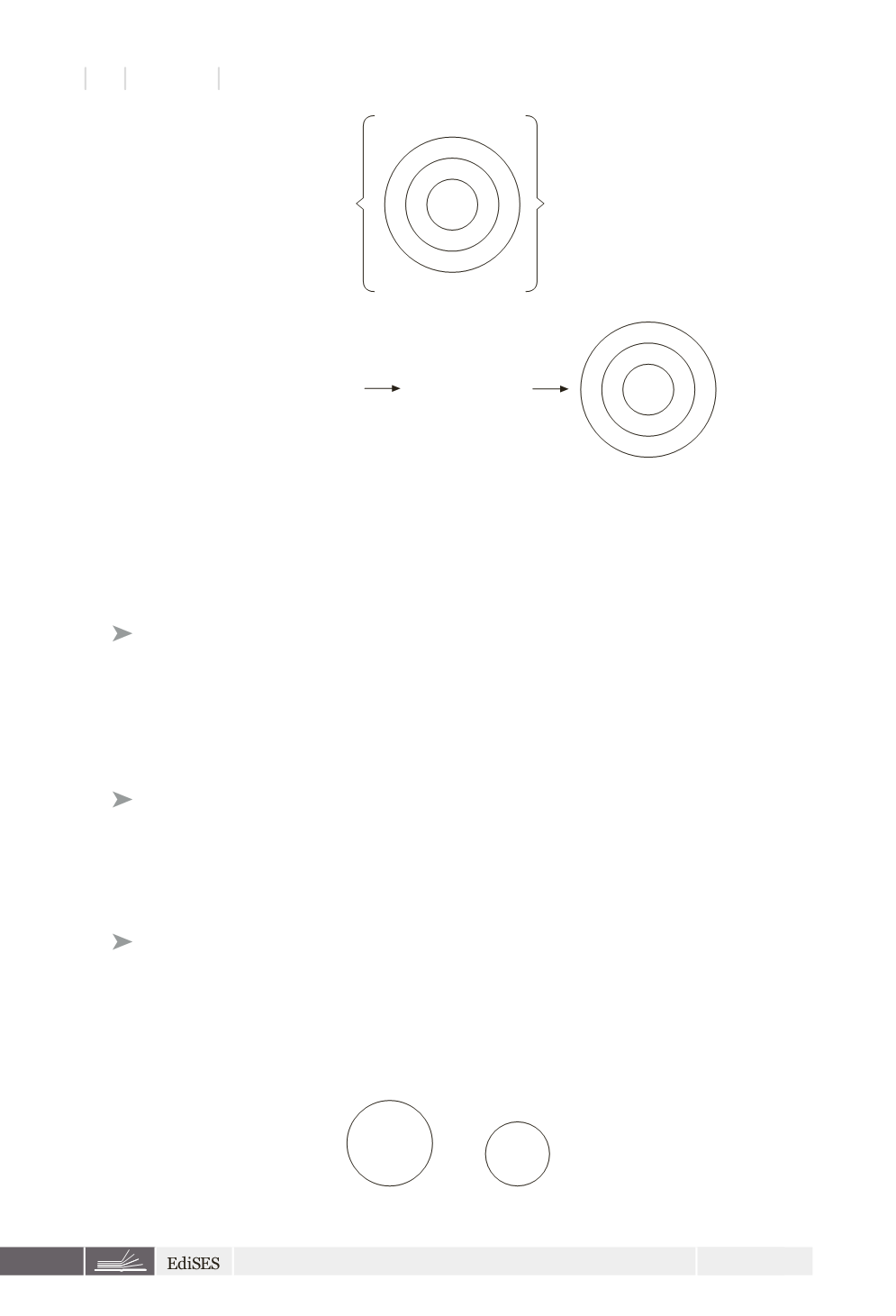
A
B
C
Tutti i
B
sono
C
Tutti gli
A
sono
B
Tutti gli A sono C
A
C
È corretto concludere che
1.2.2 c
ome
aiutarsi
con
i diagrammi
insiemistici
Gli insiemi sono gruppi di più elementi accomunati da una medesima caratteristica. Il più classi-
co dei diagrammi utilizzati è quello di Eulero-Venn, rappresentato da un cerchio (o da un’ellisse).
Esistono tre tipi di relazione che possono intercorrere fra due o più insiemi, e cioè:
–
inclusione
: si ha quando TUTTI gli elementi di un insieme sono anche elementi di un se-
condo insieme.
Se abbiamo due insiemi, italiani e bolognesi, sappiamo che tutti i bolognesi sono
anche italiani, e quindi l’insieme della categoria bolognesi è incluso in quello de-
gli italiani (uno contiene l’altro). Il diagramma è rappresentato da un cerchio den-
tro l’altro.
–
esclusione
: si ha quando NESSUN elemento di un insieme appartiene ad un secondo in-
sieme.
Se abbiamo due insiemi, napoletani e milanesi, si può agevolmente ricavare che nes-
sun napoletano è allo stesso tempo milanese, per cui i due insiemi risultano disgiun-
ti. Avremo perciò due cerchi affiancati, senza alcun punto di contatto.
–
intersezione
: si ha quandoALCUNI elementi di un insieme sono anche elementi di un se-
condo insieme.
Se abbiamo due insiemi, giovani e persone dai capelli biondi, possiamo sostenere
che alcuni giovani avranno i capelli biondi (altri castani, rossi, neri…). L’insieme dei
giovani, quindi, si interseca con quello delle persone coi capelli biondi.
La seguente figura rappresenta due gruppi di elementi distinti che non esprimono alcuna re-
lazione: il gruppo dei cani e il gruppo dei gatti.
CANI
GATTI
















