Test psico-attitudinali e Colloquio psicologico

28 / 32

192 Parte Terza I test attitudinali
www.edises.it
1.2.3 le negazioni
Le negazioni sono enunciati espressi in forma negativa, da cui bisogna dedurre la conclusio-
ne corretta. Possiamo trovarle formulate in diversi modi.
Se dico “Non tutti i biondi sono furbi”, vuol dire che qualche biondo può non esserlo. Que-
sto perché il contrario di non tutti è qualche/qualcuno.
Per lo stesso motivo, se dico “Non è vero che tutti i biondi sono furbi”, significa che alcuni
biondi non sono furbi.
Queste negazioni particolarmente semplici possono essere risolte grazie all’ausilio di uno
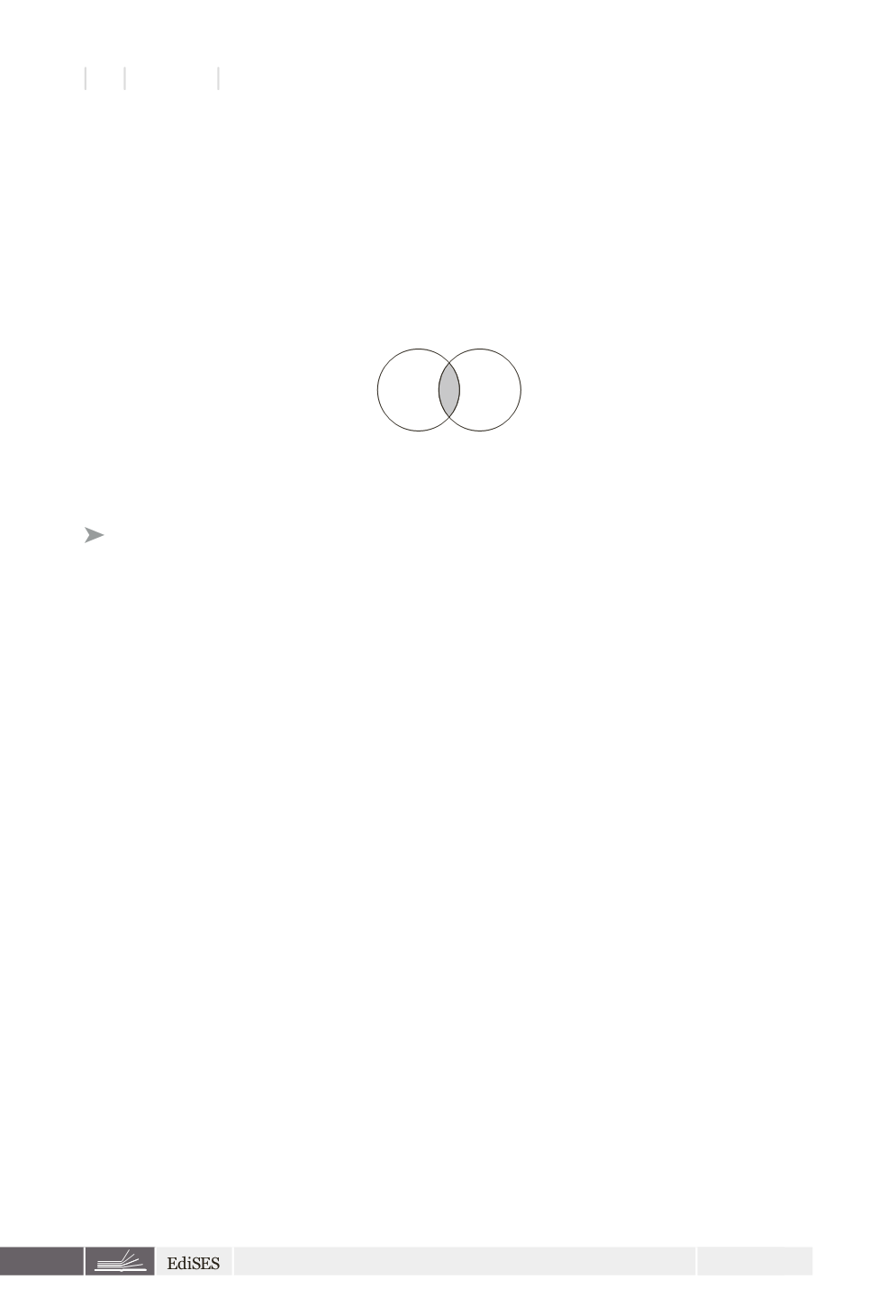
schema grafico. L’espressione può infatti essere rappresentata graficamente come segue:
B F
L’area grigia indica gli individui che presentano entrambi gli attributi. Appare subito evidente
che esiste una parte di biondi che non sono furbi ed una parte di furbi che non sono biondi.
Un signore chiese ad un filosofo di guardare dalla finestra per vedere se pioveva; il filo-
sofo per tutta risposta disse “non credo sia giusto negare che ci si sbagli nell’affermare
che è falso dire che piove!”
Pioveva o era bel tempo?
Si tratta di una tipologia di quesiti piuttosto frequente.
Se non si adottano delle strategie di risoluzione, ci si perde nel dedalo delle negazioni.
Scomponiamo la frase in tre parti:
– non credo sia giusto negare equivale a dire è giusto affermare, o meglio è vero
– che ci si sbagli nell’affermare equivale a dire che è corretto negare o meglio che ci
si sbaglia a dire
– che è falso dire che piove equivale a dire che non è vero che piove
Ricostruiamo la nuova frase in questo modo: È vero che ci si sbaglia a dire che non è
vero che piove, che potrebbe essere semplificata maggiormente elidendo la prima par-
te, … si sbaglia a dire che non è vero che piove. Ora la frase è più chiara, infatti si può
concludere che stava piovendo!
1.2.4 le deduzioni logicHe
Le deduzioni logiche in senso stretto richiedono la fondamentale distinzione tra condizione
necessaria e condizione sufficiente. Si gioca tutto su questo.
Come riconoscere la differenza? Semplice. Affinché una condizione sia necessaria basta che
la premessa inizi con la locuzione “solo se”. Facciamo un esempio per capire meglio.
“Se bevo tutto il vino contenuto nella bottiglia, resterò senza vino ”. Ebbene, la prima propo-
sizione è condizione sufficiente, ma non necessaria, affinché si realizzi anche la seconda, per-
ché la bottiglia potrebbe restare vuota anche a seguito di altri eventi, come la sua rottura ac-
cidentale. Se invece dicessimo: “ Solo se bevo tutto il vino contenuto nella bottiglia, resterò
senza vino”, allora rendo la premessa una conditio sine qua non della conclusione.