
Capitolo 1
Analisi di alcune tipologie di test attitudinali
185
www.
edises
.it
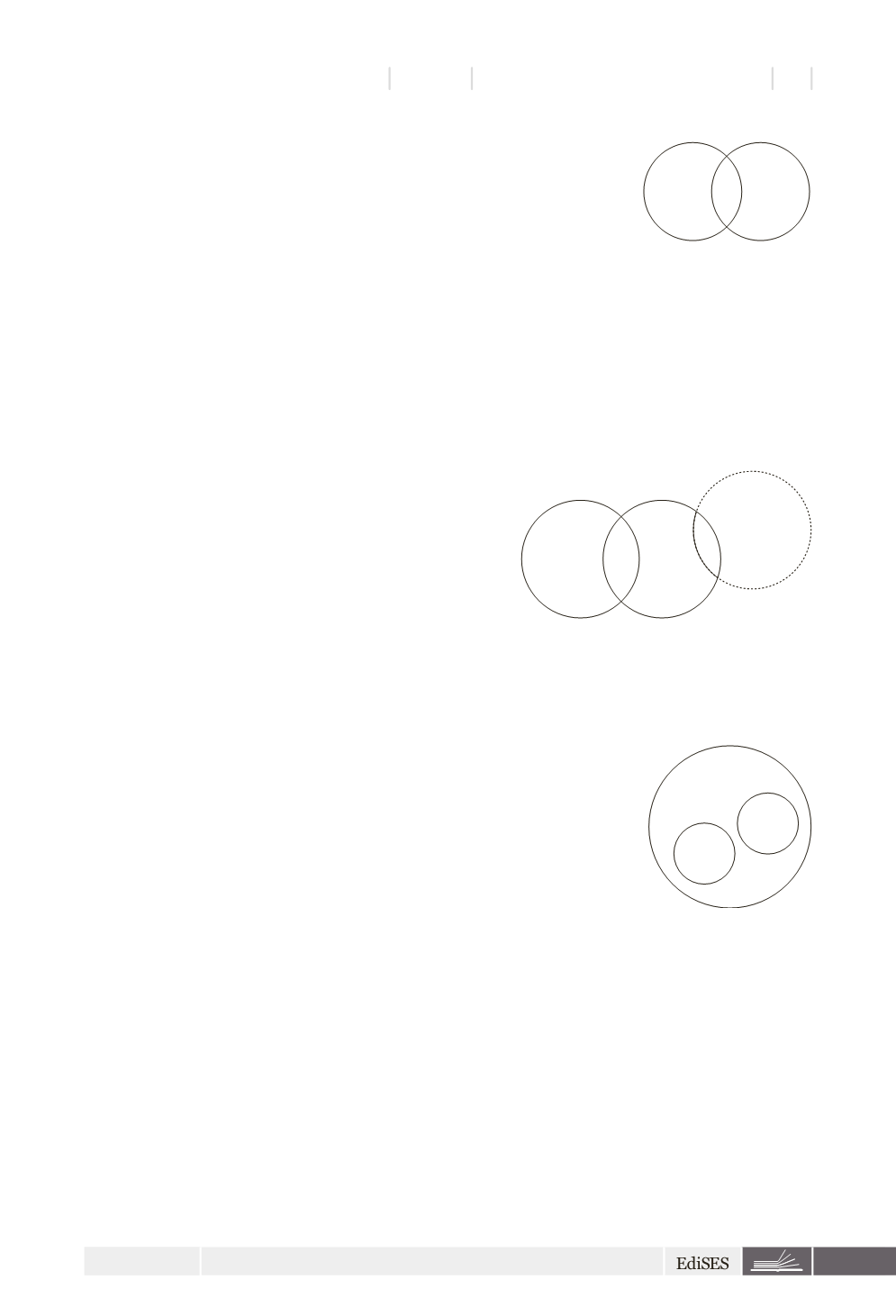
Variante particolare negativa
Alcuni A non sono B viene rappresentato come nella figura a lato.
Viene rappresentata sempre con la sovrapposizione delle due aree,
ma si pone attenzione alla parte non sovrapposta. Caratteristica di
questa variante è la
non convertibilità
.
Se la premessa particolare negativa è
Alcuni animali non sono cani
, la
conversione
Alcuni cani non sono animali
non è accettabile. Il buon ri-
solutore sa che la premessa
Alcuni animali non sono cani
implica che
Alcuni animali SONO cani
.
1.2.1.2 Errori di ragionamento
Il buon risolutore non si fa ingannare dagli errori de-
terminati dal cosiddetto
effetto “atmosfera”
.
Partendo dalle premesse:
– alcuni A sono B;
– alcuni B sono C;
si conclude che:
– alcuni A sono C.
L’errore di “atmosfera” è creato dalla comunanza del
quantificatore “alcuni” presente sia nelle due premes-
se sia nella conclusione. Il buon risolutore immagina
una configurazione come nella figura a lato non fa-
cendosi condizionare dalla superficiale affinità.
Un altro errore può derivare da una conversione illecita già accennata.
Abbiamo ricordato che le premesse universali negative e le particola-
ri affermative possono essere legittimamente convertite, mentre non
è legittima la conversione delle altre premesse.
Se consideriamo il sillogismo (universale affermativo):
– Tutti gli A sono C
– Tutti i B sono C
– Quindi, tutti gli A sono B
notiamo che non è corretto. Infatti il buon risolutore rappresenta una
configurazione come a lato a partire dalle due premesse.
L’insieme C può contenere i due sottoinsiemi A e B che tuttavia man-
tengono la loro reciproca autonomia. Per riportare l’esempio in un
contesto concreto si pensi al rapporto tra stoviglie, piatti e bicchieri.
Tutti i piatti (A) rientrano nell’insieme stoviglie (C); tutti i bicchieri
(B) rientrano nell’insieme stoviglie (C) ma non c’è alcuna sovrappo-
sizione tra i due insiemi B e A.
Se invece il sillogismo fosse stato:
– Tutti gli A sono B (oppure tutti i milanesi sono lombardi)
– Tutti i B sono C (oppure tutti i lombardi sono italiani)
– Quindi tutti gli A sono C (quindi tutti i milanesi sono italiani)
le conclusioni sarebbero da considerare accettabili?
Dalla figura riportata di seguito si capisce immediatamente la risposta.
A
B
×
×
C
Alcuni B sono C
Alcuni A sono B
A
B
C
A
B
×
















